GASES
*PROCESOS ISOTÉRMICOS
*PROCESO ISOBÁRICO
*PROCESOS ISOTÉRMICOS
*PROCESO ISOBÁRICO
GASES
Se denomina al estado de agregación de la materia en el
cual, bajo ciertas condiciones de temperatura y presión, sus moléculas
interaccionan solo débilmente entre sí, sin formar enlaces moleculares, adoptando
la forma y el volumen del recipiente que las contiene y tendiendo a separarse,
esto es, expandirse, todo lo posible por su alta energía cinética.
PROPIEDADES
DE LOS GASES
·
Las moléculas de un gas se encuentran
prácticamente libres.
·
Los gases ocupan completamente el volumen del
recipiente que los contiene.
·
Los gases no tienen forma definida, adoptando la
de los recipientes que las contiene.
·
Pueden comprimirse fácilmente, debido a que
existen enormes espacios vacíos entre unas moléculas y otras.

Historia
En 1648, el químico Jan Baptist van Helmont, considerado el
padre de la química neumática, creó el vocablo gas (durante un tiempo se usó
también "estado aeriforme"), a partir del término griego kaos
(desorden) para definir las características del anhídrido carbónico.
Esta denominación se extendió luego a todos los cuerpos
gaseosos, también llamados fluidos elásticos, fluidos compresibles o aires, y
se utiliza para designar uno de los estados de la materia.
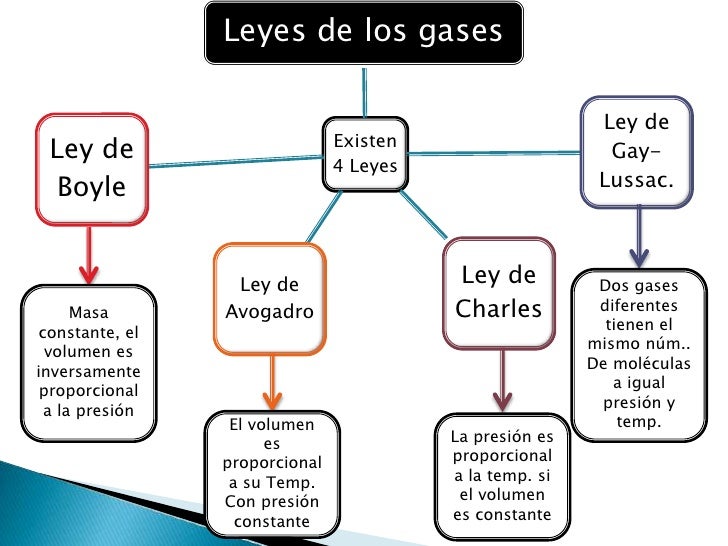
Leyes
de los gases
• Existen
diversas leyes derivadas de modelos simplificados de la realidad que relacionan
la presión, el volumen y la temperatura de un gas.
PROCESO ISOTERMICO
Definición
Ò Se
denomina proceso isotérmico o proceso isotermo al cambio
reversible en un sistema termodinámico, siendo dicho cambio a
temperatura constante en todo el sistema.
• La compresión o expansión de
un gas ideal puede
llevarse a cabo colocando el gas en contacto térmico con otro sistema de capacidad
calorífica muy grande y a la misma temperatura que el gas. este
otro sistema se conoce como foco calórico.
• El
calor se transfiere muy lentamente, permitiendo que el gas se expanda
realizando trabajo. Como la energía interna de
un gas ideal sólo depende de la temperatura y ésta permanece constante en la
expansión isoterma, el calor tomado del foco es igual al trabajo realizado por
el gas: Q = W.
• Una
curva isoterma es una línea que sobre un diagrama representa los
valores sucesivos de las diversas variables de un sistema en un proceso
isotermo. Las isotermas de un gas ideal en un diagrama P-V,
llamado diagrama de Clapeyron, son hipérbolas equiláteras, cuya ecuación
es P•V = constante.
Proceso
isotérmico de un gas
Una expansión isotérmica es un proceso en el cual
un gas se expande (o contrae), manteniendo la temperatura constante durante
dicho proceso, es decir que T1 = T2 para los estados inicial (1) y
final (2) del proceso isotérmico. Aplicando el primer principio de la
termodinámica se obtiene
Ondas
Una onda
transversal
En una onda
transversal, la vibración de las partículas individuales del medio es
perpendicular a la dirección de propagación de la onda.
Ondas
longitudinales
En una onda
longitudinal, la vibración de las partículas individuales es paralela a la
dirección de propagación de la onda.

Olas
Una ola
oceánica es una combinación de transversal y longitudinal.
Las
partículas individuales se mueven en elipses conforme la perturbación de la
onda se mueve hacia la playa.
Rapidez de
onda en una cuerda.
La rapidez
de onda v en una cuerda en vibración se determina mediante la tensión F
y la densidad lineal m, o masa por unidad de longitud.
Ejemplo 1: Una sección de 5 g de cuerda tiene una
longitud de 2 m desde la pared hasta lo alto de una polea. Una masa de 200 g
cuelga en el extremo. ¿Cuál es la rapidez de una onda en esta cuerda?
F = (0.20
kg)(9.8 m/s2) = 1.96 N
SONIDO

u Es cualquier fenómeno que
involucre la propagación en forma de ondas elásticas (sean audibles
o no), generalmente a través de un fluido (u otro medio elástico) que esté
generando el movimiento vibratorio de un cuerpo.

u Velocidad del sonido
u En el aire, el sonido tiene una velocidad
de 331,5 m/s cuando: la temperatura es de 0 °C, la presión
atmosférica es de 1 atm (nivel del mar) y se presenta una humedad relativa
del aire de 0 % (aire seco). Aunque depende muy poco de la presión del
aire.
u La velocidad del sonido depende del tipo
de material. Cuando el sonido se desplaza en los sólidos tiene mayor velocidad
que en los líquidos, y en los líquidos es más veloz que en los gases. Esto se
debe a que las partículas en los sólidos están más cercanas.
FORMULAS

El eco es un fenómeno acústico producido cuando una onda se refleja y regresa hacia su emisor. Puede referirse tanto a ondas sonoras como a electromagnéticas. El efecto acústico producido por la reflexión del sonido una vez acabada su primera exposición.
En el caso del oído humano, para que sea percibido es necesario que el eco supere la persistencia acústica, en caso contrario el cerebro interpreta el sonido emitido y el reflejado como un mismo sonido. El mínimo retardo necesario entre ambos sonidos varía desde alrededor de 100 ms para sonidos secos hasta varios segundos para sonidos complejos, como la música. Si el sonido ha sido deformado hasta hacerse irreconocible, se denomina reverberación en vez de eco.
El caso de las ondas electromagnéticas, el fenómeno es utilizado en el radar.
Proceso isocórico
Un proceso isocórico, también llamado proceso isométrico o isovolumétrico es un proceso termodinámico en el cual el volumen permanece constante; 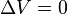 . Esto implica que el proceso no realiza trabajo presión-volumen, ya que éste se define como:
. Esto implica que el proceso no realiza trabajo presión-volumen, ya que éste se define como:
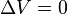 . Esto implica que el proceso no realiza trabajo presión-volumen, ya que éste se define como:
. Esto implica que el proceso no realiza trabajo presión-volumen, ya que éste se define como: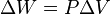 ,
,
donde P es la presión (el trabajo es positivo, ya que es ejercido por el sistema).
En un diagrama P-V, un proceso isocórico aparece como una línea vertical.
Es un proceso a volumen constante, en consecuencia.
W = 0, y tendremos:
En un recipiente de paredes gruesas que contiene un gas determinado, al que se le suministra calor, observamos que la temperatura y presión interna se elevan, pero el volumen se mantiene igual.
W = 0, y tendremos:
En un recipiente de paredes gruesas que contiene un gas determinado, al que se le suministra calor, observamos que la temperatura y presión interna se elevan, pero el volumen se mantiene igual.
En un proceso que se efectúa a volumen constante sin que haya ningún desplazamiento, el trabajo hecho por el sistema es cero.
Es decir, en un proceso isocórico no hay trabajo realizando por el sistema. Y no se adiciona calor al sistema que ocasione un incremento de su energía interna.


Proceso adiabático
En termodinámica se designa como proceso adiabático a aquel en el cual el sistema termodinámico (generalmente, un fluido que realiza un trabajo) no intercambia calor con su entorno. Un proceso adiabático que es además reversible se conoce como proceso isentrópico. El extremo opuesto, en el que tiene lugar la máxima transferencia de calor, causando que la temperatura permanezca constante, se denominaproceso isotérmico.
El término adiabático hace referencia a volúmenes que impiden la transferencia de calor con el entorno. Una pared aislada se aproxima bastante a un límite adiabático. Otro ejemplo es la temperatura adiabática de llama, que es la temperatura que podría alcanzar una llama si no hubiera pérdida de calor hacia el entorno. En climatización los procesos de humectación (aporte de vapor de agua) son adiabáticos, puesto que no hay transferencia de calor, a pesar que se consiga variar la temperatura del aire y su humedad relativa.
El calentamiento y enfriamiento adiabático son procesos que comúnmente ocurren debido al cambio en la presión de un gas. Esto puede ser cuantificado usando la ley de los gases ideales.
En otras palabras se considera proceso adiabático a un sistema especial en el cual no se pierde ni tampoco se gana energía calorífica. Esto viene definido según la primera ley de termodinámica describiendo que Q=0
Si se relaciona el tema del proceso adiabático con las ondas, se debe tener en cuenta que el proceso o carácter adiabático solo se produce en las ondas longitudinales
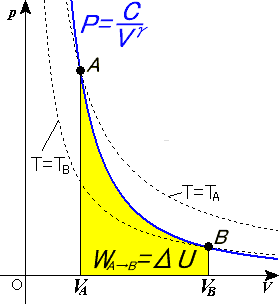
La ecuación matemática que describe un proceso adiabático en un gas (si el proceso es reversible) es
donde P es la presión del gas, V su volumen y
el coeficiente adiabático, siendo  el calor específico molar a presión constante y
el calor específico molar a presión constante y  el calor específico molar a volumen constante. Para un gas monoatómico ideal,
el calor específico molar a volumen constante. Para un gas monoatómico ideal, 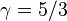 . Para un gas diatómico (como el nitrógeno o el oxígeno, los principales componentes del aire)
. Para un gas diatómico (como el nitrógeno o el oxígeno, los principales componentes del aire) 
 el calor específico molar a presión constante y
el calor específico molar a presión constante y  el calor específico molar a volumen constante. Para un gas monoatómico ideal,
el calor específico molar a volumen constante. Para un gas monoatómico ideal, 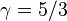 . Para un gas diatómico (como el nitrógeno o el oxígeno, los principales componentes del aire)
. Para un gas diatómico (como el nitrógeno o el oxígeno, los principales componentes del aire) 
Derivación de la expresión[editar]
La definición de un proceso adiabático es que la transferencia de calor del sistema es cero,  .
.
 .
.
Por lo que de acuerdo con el primer principio de la termodinámica,
donde U es la energía interna del sistema y W es el trabajo realizado por el sistema. Cualquier trabajo (W) realizado debe ser realizado a expensas de la energía U, mientras que no haya sido suministrado calor Q desde el exterior. El trabajo W realizado por el sistema se define como
Sin embargo, P no permanece constante durante el proceso adiabático sino que por el contrario cambia junto con V.
en la fórmula:
hacemos un pequeño cambio entonces quedaría así:
 ......(1)
......(1)
Ahora derivando la fórmula de del trabajo e integrándola a la vez tenemos :
 =
= .....(2)
.....(2)
Ahora reemplazamos la (2) en la (1) :

Ahora sabemos que "K" es una constante , por lo cual esta sale de la integral:

luego vemos que nos queda todo en función del volumen entonces lo integramos:

como sabemos que :

entonces reemplazamos en la ecuación:

y multiplicamos :

luego de resolver la ecuación nos quedará esta forma:
![[P_{2}*V_{2}-P_{1}*V_{1}]/(1-{\gamma})\qquad](https://upload.wikimedia.org/math/1/2/e/12e0bc4e9cc3f701deb42d07a2905b02.png)
y por definición nos quedaría :
que al final nos dará:

y esto será igual al trabajo :

también podemos tener una variante :
Deseamos conocer cómo los valores de  y
y  se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que
se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que
 y
y  se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que
se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que
donde R es la constante universal de los gases.
Dado  y
y  entonces
entonces  y
y
 y
y  entonces
entonces  y
y
Ahora sustituyendo las ecuaciones (2) y (3) en la ecuación (1) obtenemos
simplificando
dividiendo ambos lados de la igualdad entre PV
Aplicando las normas del cálculo diferencial obtenemos que
que se puede expresar como
Para ciertas constantes 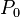 y
y  del estado inicial. Entonces
del estado inicial. Entonces
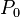 y
y  del estado inicial. Entonces
del estado inicial. Entonces
elevando al exponente ambos lados de la igualdad
eliminando el signo menos
por lo tanto
y
PROCESO DIATERMICO
· Un proceso diatérmico quiere decir que deja pasar el calor fácilmente.
· Una interacción térmica es cualquier otro tipo de intercambio de energía. En este caso la pared se denomina diatérmica.
· Diatérmico también puede entenderse por isotérmico , significa que no hay cambio de temperatura debido a una pared diatérmica que aísla el sistema del medio ambiente
· En cuanto diatérmicos se refieren a que el sistema tiene un intercambio de energía con los alrededores, un ejemplo, nosotros, los seres humanos, somos sistemas diatérmicos, ya que estamos intercambiando energía con nuestro ambiente
· Una pared diatérmica es aquella que permite la transferencia de energía térmica (calor) pero, sin que haya transferencia de masa. El opuesto es una pared adiabática que es la que impide la transferencia de energía en forma de calor.
· Cualquier superficie real es una superficie diatérmica, por ejemplo, un vaso, los muros de una casa, etc., todos en mayor o menor grado permiten la transferencia de calor.





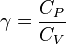
















No hay comentarios:
Publicar un comentario