luz
La
óptica es la rama de la física que estudia el comportamiento de la luz, sus características y sus manifestaciones.
Velocidad finita[editar]
Se ha demostrado teórica y experimentalmente que la luz tiene una velocidad finita. La primera medición con éxito fue hecha por el astrónomo danés
Ole Roemer en
1676 y desde entonces numerosos experimentos han mejorado la precisión con la que se conoce el dato. Actualmente el valor exacto aceptado para la velocidad de la luz en el vacío es de 299 792 458
m/s.
1
La velocidad de la luz al propagarse a través de la materia es menor que a través del vacío y depende de las propiedades dieléctricas del medio y de la energía de la luz. La relación entre la velocidad de la luz en el vacío y en un medio se denomina
índice de refracción del medio:


La línea amarilla muestra el tiempo que tarda la luz en recorrer el espacio entre la
Tierra y la
Luna, alrededor de 1,26 segundos.
Refracción

En esta ilustración se muestra la descomposición de la luz al atravesar un
prisma.
La
refracción es el variación brusca de dirección que sufre la luz al cambiar de medio. Este fenómeno se debe al hecho de que la luz se propaga a diferentes velocidades según el medio por el que viaja. El cambio de dirección es mayor cuanto mayor es el cambio de velocidad, ya que la luz recorre mayor distancia en su desplazamiento por el medio en que va más rápido. La
ley de Snell relaciona el cambio de ángulo con el cambio de velocidad por medio de los
índices de refracción de los medios.
Como la refracción depende de la energía de la luz, cuando se hace pasar luz blanca o policromática a través de un medio con caras no paralelas, como un
prisma, se produce la separación de la luz en sus diferentes componentes (colores) según su energía, en un fenómeno denominado
dispersión refractiva. Si el medio tiene las caras paralelas, la luz se vuelve a recomponer al salir de él.
Ejemplos muy comunes de la refracción es la ruptura aparente que se ve en un lápiz al introducirlo en agua o el
arcoíris.
Propagación y difracciónA
Una de las propiedades de la luz más evidentes a simple vista es que se propaga en línea
recta. Lo podemos ver, por ejemplo, en la propagación de un rayo de luz a través de ambientes polvorientos o de atmósferas saturadas. La
óptica geométrica parte de esta premisa para predecir la posición de la luz, en un determinado momento, a lo largo de su transmisión.
De la propagación de la luz y su encuentro con objetos surgen las
sombras. Si interponemos un cuerpo
opaco en el camino de la luz y a continuación una pantalla, obtendremos sobre ella la sombra del cuerpo. Si el origen de la luz o
foco se encuentra lejos del cuerpo, de tal forma que, relativamente, sea más pequeño que el cuerpo, se producirá una sombra definida. Si se acerca el foco al cuerpo surgirá una sombra en la que se distinguen una región más clara denominada
penumbra y otra más oscura denominada
umbra.
Sin embargo, la luz no siempre se propaga en línea recta. Cuando la luz atraviesa un obstáculo puntiagudo o una abertura estrecha, el rayo se curva ligeramente. Este fenómeno, denominado
difracción, es el responsable de que al mirar a través de un agujero muy pequeño todo se vea distorsionado o de que los telescopios y microscopios tengan un número de aumentos máximo limitado.
Interferencia
La forma más sencilla de estudiar el fenómeno de la interferencia es con el denominado
experimento de Young que consiste en hacer incidir luz
monocromática (de un solo color) en una pantalla que tiene una rendija muy estrecha. La luz difractada que sale de dicha rendija se vuelve a hacer incidir en otra pantalla con una doble rendija. La luz procedente de las dos rendijas se combina en una tercera pantalla produciendo bandas alternativas claras y oscuras.
El fenómeno de las interferencias se puede ver también de forma natural en las manchas de aceite sobre los charcos de agua o en la cara con información de los
discos compactos; ambos tienen una
superficie que, cuando se ilumina con luz blanca, la
difracta, produciéndose una cancelación por interferencias, en función del ángulo de incidencia de la luz, de cada uno de los colores que contiene, permitiendo verlos separados, como en un
arco iris.
Reflexión y dispersión
Al incidir la luz en un cuerpo, la materia de la que está constituido retiene unos instantes su
energía y a continuación la reemite en todas las direcciones. Este fenómeno es denominado
reflexión. Sin embargo, en superficies ópticamente lisas, debido a
interferencias destructivas, la mayor parte de la radiación se pierde, excepto la que se propaga con el mismo ángulo que incidió. Ejemplos simples de este efecto son los
espejos, los metales pulidos o el agua de un río (que tiene el fondo oscuro).
La luz también se refleja por medio del fenómeno denominado
reflexión interna total, que se produce cuando un rayo de luz, intenta salir de un medio en que su velocidad es más lenta a otro más rápido, con un determinado ángulo. Se produce una
refracción de tal modo que no es capaz de atravesar la superficie entre ambos medios reflejándose completamente. Esta reflexión es la responsable de los destellos en un
diamante tallado.
En el vacío, la velocidad es la misma para todas las longitudes de onda del espectro visible, pero cuando atraviesa sustancias materiales la velocidad se reduce y varía para cada una de las distintas longitudes de onda del espectro, este efecto se denomina
dispersión. Gracias a este fenómeno podemos ver los colores del arcoíris. El color azul del cielo se debe a la luz del
sol dispersada por la
atmósfera. El color blanco de las
nubes o el de la
leche también se debe a la dispersión de la luz por las gotitas de
agua o por las partículas de grasa en suspensión que contienen respectivamente.
Polarización
El fenómeno de la
polarización se observa en unos cristales determinados que individualmente son transparentes. Sin embargo, si se colocan dos en serie, paralelos entre sí y con uno girado un determinado ángulo con respecto al otro, la luz no puede atravesarlos. Si se va rotando uno de los cristales, la luz empieza a atravesarlos alcanzándose la máxima intensidad cuando se ha rotado el cristal 90°
sexagesimales respecto al ángulo de total
oscuridad.
También se puede obtener luz polarizada a través de la
reflexión de la luz. La luz reflejada está parcial o totalmente polarizada dependiendo del ángulo de incidencia. El ángulo que provoca una polarización total se llama
ángulo de Brewster.
Muchas
gafas de sol y filtros para
cámaras incluyen cristales polarizadores para eliminar reflejos molestos.
Efectos químicos
Algunas sustancias al absorber luz, sufren
cambios químicos; utilizan la
energía que la luz les transfiere para alcanzar los niveles energéticos necesarios para reaccionar, para obtener una conformación estructural más adecuada para llevar a cabo una reacción o para romper algún enlace de su estructura (
fotólisis).
Aproximación histórica
A principios del
siglo XVIII era creencia generalizada que la luz estaba compuesta de pequeñas partículas. Fenómenos como la reflexión, la refracción y las
sombras de los cuerpos, se podían esperar de torrentes de partículas.
Isaac Newton demostró que la refracción estaba provocada por el cambio de velocidad de la luz al cambiar de medio y trató de explicarlo diciendo que las partículas aumentaban su velocidad al aumentar la densidad del medio. La comunidad científica, consciente del prestigio de Newton, aceptó su teoría corpuscular.
En la cuneta quedaba la teoría de
Christian Huygens que en
1678 propuso que la luz era un fenómeno ondulatorio que se transmitía a través de un medio llamado
éter. Esta teoría quedó olvidada hasta la primera mitad del
siglo XIX, cuando
Thomas Young solo era capaz de explicar el fenómeno de las interferencias suponiendo que la luz fuese en realidad una onda. Otros estudios de la misma época explicaron fenómenos como la difracción y la polarización teniendo en cuenta la teoría ondulatoria.
El golpe final a la teoría corpuscular pareció llegar en
1848, cuando se consiguió medir la velocidad de la luz en diferentes medios y se encontró que variaba de forma totalmente opuesta a como lo había supuesto Newton. Debido a esto, casi todos los científicos aceptaron que la luz tenía una naturaleza ondulatoria. Sin embargo todavía quedaban algunos puntos por explicar como la propagación de la luz a través del vacío, ya que todas las ondas conocidas se desplazaban usando un medio físico, y la luz viajaba incluso más rápido que en el aire o el agua. Se suponía que este medio era el éter del que hablaba Huygens, pero nadie lo conseguía encontrar.
En
1845,
Michael Faraday descubrió que el ángulo de polarización de la luz se podía modificar aplicándole un campo magnético (
efecto Faraday), proponiendo dos años más tarde que la luz era una vibración electromagnética de alta frecuencia.
James Clerk Maxwell, inspirado por el trabajo de Faraday, estudió matemáticamente estas ondas electromagnéticas y se dio cuenta de que siempre se propagaban a una velocidad constante, que coincidía con la velocidad de la luz, y de que no necesitaban medio de propagación ya que se autopropagaban. La confirmación experimental de las teorías de Maxwell eliminó las últimas dudas que se tenían sobre la naturaleza ondulatoria de la luz.
No obstante, a finales del
siglo XIX, se fueron encontrando nuevos efectos que no se podían explicar suponiendo que la luz fuese una onda, como, por ejemplo, el
efecto fotoeléctrico, esto es, la emisión de electrones de las superficies de sólidos y líquidos cuando son iluminados. Los trabajos sobre el proceso de absorción y emisión de energía por parte de la materia solo se podían explicar si uno asumía que la luz se componía de partículas. Entonces la ciencia llegó a un punto muy complicado e incomodo: se conocían muchos efectos de la luz, sin embargo, unos solo se podían explicar si se consideraba que la luz era una onda, y otros solo se podían explicar si la luz era una partícula.
El intento de explicar esta dualidad onda-partícula, impulsó el desarrollo de la física durante el
siglo XX. Otras ciencias, como la
biología o la
química, se vieron revolucionadas ante las nuevas teorías sobre la luz y su relación con la materia.
Naturaleza de la luz
La luz presenta una naturaleza compleja: depende de cómo la observemos se manifestará como una
onda o como una
partícula. Estos dos estados no se excluyen, sino que son complementarios (véase
Dualidad onda corpúsculo). Sin embargo, para obtener un estudio claro y conciso de su naturaleza, podemos clasificar los distintos fenómenos en los que participa según su interpretación teórica:
Teoría ondulatoria
Esta teoría, desarrollada por
Christiaan Huygens, considera que la luz es una
onda electromagnética, consistente en un
campo eléctrico que varía en el tiempo generando a su vez un
campo magnético y viceversa, ya que los campos eléctricos variables generan campos magnéticos (
ley de Ampère) y los campos magnéticos variables generan campos eléctricos (
ley de Faraday). De esta forma, la onda se autopropaga indefinidamente a través del espacio, con campos magnéticos y eléctricos generándose continuamente. Estas ondas electromagnéticas son
sinusoidales, con los campos eléctrico y magnético perpendiculares entre sí y respecto a la dirección de propagación.

Vista lateral (izquierda) de una onda electromagnética a lo largo de un instante y vista frontal (derecha) de la misma en un momento determinado. De color rojo se representa el campo magnético y de azul el eléctrico.
Para poder describir una onda electromagnética podemos utilizar los parámetros habituales de cualquier
onda:
- Amplitud (A): Es la longitud máxima respecto a la posición de equilibrio que alcanza la onda en su desplazamiento.
- Periodo (T): Es el tiempo necesario para el paso de dos máximos o mínimos sucesivos por un punto fijo en el espacio.
- Frecuencia (ν): Número de oscilaciones del campo por unidad de tiempo. Es una cantidad inversa al periodo.
- Longitud de onda (λ): Es la distancia lineal entre dos puntos equivalentes de ondas sucesivas.
- Velocidad de propagación (V): Es la distancia que recorre la onda en una unidad de tiempo. En el caso de la velocidad de propagación de la luz en el vacío, se representa con la letra c.
La velocidad, la frecuencia, el periodo y la longitud de onda están relacionadas por las siguientes ecuaciones:
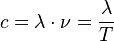
Fenómenos ondulatorios[editar]
Algunos de los fenómenos más importantes de la luz se pueden comprender fácilmente si se considera que tiene un comportamiento ondulatorio.
El
principio de superposición de ondas nos permite explicar el fenómeno de la
interferencia: si juntamos en el mismo lugar dos ondas con la misma longitud de onda y amplitud, si están en fase (las crestas de las ondas coinciden) formarán una
interferencia constructiva y la intensidad de la onda resultante será máxima e igual a dos veces la amplitud de las ondas que la conforman. Si están desfasadas, habrá un punto donde el desfase sea máximo (la cresta de la onda coincida exactamente con un valle) formándose una
interferencia destructiva, anulándose la onda. El
experimento de Young, con sus rendijas, nos permite obtener dos focos de luz de la misma longitud de onda y amplitud, creando un patrón de interferencias sobre una pantalla.
Las ondas cambian su dirección de propagación al cruzar un obstáculo puntiagudo o al pasar por una abertura estrecha. Como recoge el
principio de Fresnel - Huygens, cada punto de un frente de ondas es un emisor de un nuevo frente de ondas que se propagan en todas las direcciones. La suma de todos los nuevos frentes de ondas hace que la perturbación se siga propagando en la dirección original. Sin embargo, si por medio de una rendija o de un obstáculo puntiagudo, se separa uno o unos pocos de los nuevos emisores de ondas, predominará la nueva dirección de propagación frente a la original.

Onda propagándose a través de una rendija.
La
difracción de la luz se explica fácilmente si se tiene en cuenta este efecto exclusivo de las ondas. La
refracción, también se puede explicar utilizando este
principio, teniendo en cuenta que los nuevos frentes de onda generados en el nuevo medio, no se transmitirán con la misma velocidad que en el anterior medio, generando una distorsión en la dirección de propagación:
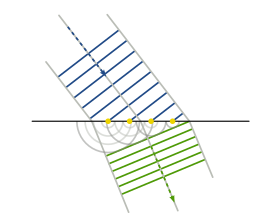
Refracción de la luz según el principio de Huygens.
Otro fenómeno de la luz fácilmente identificable con su naturaleza ondulatoria es la
polarización. La luz no polarizada está compuesta por ondas que vibran en todos los ángulos, al llegar a un medio polarizador, solo las ondas que vibran en un ángulo determinado consiguen atravesar el medio, al poner otro polarizador a continuación, si el ángulo que deja pasar el medio coincide con el ángulo de vibración de la onda, la luz pasará íntegra, si no solo una parte pasará hasta llegar a un ángulo de 90º entre los dos polarizadores, donde no pasará nada de luz.

Dos polarizadores en serie.
Este efecto, además, permite demostrar el carácter transversal de la luz (sus ondas vibran en dirección perpendicular a la dirección de propagación).

confirman que las ondas de las que está compuesta la luz son de naturaleza electromagnética. Esta teoría fue capaz, también, de eliminar la principal objeción a la teoría ondulatoria de la luz, que era encontrar la manera de que las ondas se trasladasen sin un medio material.
Teoría corpuscular
Descripción
La teoría corpuscular estudia la luz como si se tratase de un torrente de partículas sin
carga y sin
masa llamadas
fotones, capaces de transportar todas las formas de radiación electromagnética. Esta interpretación resurgió debido a que, la luz, en sus interacciones con la materia, intercambia energía solo en cantidades discretas (múltiplos de un valor mínimo) de energía denominadas
cuantos. Este hecho es difícil de combinar con la idea de que la energía de la luz se emita en forma de ondas, pero es fácilmente visualizado en términos de corpúsculos de luz o fotones.
Fenómenos corpusculares
Existen tres efectos que demuestran el carácter corpuscular de la luz. Según el orden histórico, el primer efecto que no se pudo explicar por la concepción ondulatoria de la luz fue
la radiación del cuerpo negro.
Un
cuerpo negro es un
radiador teóricamente perfecto que absorbe toda la luz que incide en él y por eso, cuando se calienta se convierte en un emisor ideal de
radiación térmica, que permite estudiar con claridad el proceso de intercambio de energía entre radiación y materia. La distribución de frecuencias observadas de la radiación emitida por la caja a una temperatura de la cavidad dada, no se correspondía con las predicciones teóricas de la física clásica. Para poder explicarlo,
Max Planck, al comienzo del
siglo XX, postuló que para ser descrita correctamente, se tenía que asumir que la luz de frecuencia ν es absorbida por múltiplos enteros de un cuanto de energía igual a
hν, donde
h es una constante física universal llamada
Constante de Planck.
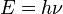
En
1905,
Albert Einstein utilizó la teoría cuántica recién desarrollada por Planck para explicar otro fenómeno no comprendido por la física clásica:
el efecto fotoeléctrico. Este efecto consiste en que cuando un rayo
monocromático de radiación electromagnética ilumina la superficie de un sólido (y, a veces, la de un líquido), se desprenden electrones en un fenómeno conocido como
fotoemisión o efecto fotoeléctrico externo. Estos electrones poseen una
energía cinética que puede ser medida electrónicamente con un colector con carga negativa conectado a la superficie emisora. No se podía entender que la emisión de los llamados "
fotoelectrones" fuese inmediata e independiente de la intensidad del rayo. Eran incluso capaces de salir despedidos con intensidades extremadamente bajas, lo que excluía la posibilidad de que la superficie acumulase de alguna forma la energía suficiente para disparar los electrones. Además, el número de electrones era proporcional a la intensidad del rayo incidente. Einstein demostró que el efecto fotoeléctrico podía ser explicado asumiendo que la luz incidente estaba formada de fotones de energía
hν, parte de esta energía
hν0 se utilizaba para romper las fuerzas que unían el electrón con la materia, el resto de la energía aparecía como la energía cinética de los electrones emitidos:
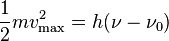
donde m es la masa del electrón, vmáx la velocidad máxima observada, ν es la frecuencia de la luz iluminante y ν0 es la frecuencia umbral característica del sólido emisor.
La demostración final fue aportada por
Arthur Compton que observó como al hacer incidir
rayos X sobre elementos ligeros, estos se
dispersaban con menor energía y además se desprendían electrones (fenómeno posteriormente denominado en su honor como
efecto Compton). Compton, ayudándose de las teorías anteriores, le dio una explicación satisfactoria al problema tratando la luz como partículas que chocan elásticamente con los electrones como dos bolas de billar. El
fotón, corpúsculo de luz, golpea al electrón: el electrón sale disparado con una parte de la energía del fotón y el fotón refleja su menor energía en su frecuencia. Las direcciones relativas en las que salen despedidos ambos están de acuerdo con los cálculos que utilizan la conservación de la energía y el momento.
Teorías cuánticas
Paul Dirac dio el primer paso con su
ecuación de ondas que aportó una síntesis de las teorías ondulatoria y corpuscular, ya que siendo una ecuación de ondas electromagnéticas su solución requería ondas cuantizadas, es decir, partículas. Su ecuación consistía en reescribir las
ecuaciones de Maxwell de tal forma que se pareciesen a las
ecuaciones hamiltonianas de la mecánica clásica. A continuación, utilizando el mismo formalismo que, a través de la introducción del cuanto de acción hν, transforma las ecuaciones de mecánica clásica en ecuaciones de mecánica ondulatoria, Dirac obtuvo una nueva ecuación del campo electromagnético. Las soluciones a esta ecuación requerían ondas cuantizadas, sujetas al
principio de incertidumbre de Heisenberg, cuya superposición representaban el
campo electromagnético. Gracias a esta ecuación podemos conocer una descripción de la probabilidad de que ocurra una interacción u observación dada, en una región determinada.
Existen aún muchas dificultades teóricas sin resolverse, sin embargo, la incorporación de nuevas teorías procedentes de la experimentación con
partículas elementales, así como de teorías sobre el comportamiento de los
núcleos atómicos, nos han permitido obtener una formulación adicional de gran ayuda.
Efectos relativísticos
Sin embargo, existían aún algunas situaciones en las que la luz no se comportaba según lo esperado por las teorías anteriores.
Luz en movimiento
La primera de estas situaciones inexplicables se producía cuando la luz se emitía, se transmitía o se recibía por cuerpos o medios en movimiento. Era de esperar, según la física clásica, que la velocidad en estos casos fuese el resultado de sumar a la
velocidad de la luz, la velocidad del cuerpo o del medio. Sin embargo, se encontraron varios casos en los que no era así:
En 1818,
Augustin Fresnel propuso un experimento para medir la velocidad a la que la luz atravesaba un líquido en movimiento. Para ello, se haría atravesar a la luz una columna de un líquido que fluyese a una velocidad
v relativa al observador. Conociendo la velocidad
v' a la que se trasmite la luz a través de ese medio, a través del
índice de refracción (n), se calculó que la velocidad total de la luz en ese fluido sería:

Sin embargo, cuando en 1851, el físico francés
Hippolyte Fizeau llevó a cabo el experimento, comprobó que la velocidad a la que la luz atravesaba el líquido en movimiento no era la calculada sino:

es decir, que la velocidad del fluido contaba menos en la velocidad final si la velocidad con la que atravesaba la luz ese fluido era mayor.
En
1725,
James Bradley descubrió que la posición observada de las estrellas en el firmamento variaba anualmente con respecto a la posición real en un intervalo de 41 segundos de
arco. La teoría que propuso para explicarlo fue que esta variación se debía a la combinación de la velocidad de la tierra al rotar alrededor del sol con la velocidad finita de la luz. Gracias a esta teoría fue capaz de calcular la velocidad de la luz de una forma aceptable. Basándose en este efecto, el astrónomo inglés
George Airy comparó el ángulo de aberración en un telescopio antes y después de llenarlo de agua, y descubrió que, en contra de sus expectativas, no había diferencia en sus mediciones (la luz no variaba de velocidad a pesar de que el fluido se movía a la velocidad de la tierra).
Teniendo en cuenta este experimento, dos astrónomos, el alemán
Albert Michelson y el estadounidense
Edward Morley propusieron un experimento (véase
Experimento de Michelson y Morley) para medir la velocidad a la que fluía el
éter con respecto a la tierra. Suponían que el éter se movía en una dirección concreta con una velocidad determinada, por eso, debido a la translación de la Tierra alrededor del Sol habría épocas del año en el que tendríamos una componente de esa velocidad a favor y otras épocas en contra, por lo que supusieron que cuando lo tuviésemos a favor, la velocidad de la luz sería superior y cuando lo tuviésemos en contra sería inferior. Para ello midieron la velocidad de la luz en diferentes estaciones del año y observaron que no había ninguna diferencia. Y lo más curioso: que ni siquiera había diferencias debidas a la propia velocidad de translación de la Tierra (30 km/s).
Distorsiones espectrales
Al comparar el
espectro de la luz procedente de algunos cuerpos celestes, con los espectros medidos en el laboratorio de los mismos elementos que los que contienen esos cuerpos, se observa que no son iguales, ya que las líneas espectrales procedentes del espacio están desplazadas hacia posiciones de mayor longitud de onda, es decir, hacia el lado rojo del espectro en lugares de menor energía.
Se han encontrado dos tipos diferentes de desplazamientos de líneas espectrales:
- Desplazamiento nebular
Uno, el más común, llamado
desplazamiento nebular es un desplazamiento sistemático de los espectros procedentes de las estrellas y galaxias.
Edwin Hubble tras estudiar el corrimiento de los espectros de las nebulosas, lo interpretó como el resultado del
efecto Doppler debido a la expansión continua del
universo. Gracias a esto propuso una fórmula capaz de calcular la distancia que nos separa de un cuerpo determinado analizando el corrimiento de su espectro:

Reflexión
Para otros usos de este término, véase
Reflexión.

Reflejo de unas rocas en el mar.

Láser reflectado usando un semidisco de lucita, Foto tomada en el laboratorio de óptica de la facultad de ciencias de la unam.
La
reflexión es el cambio de dirección de una
onda, que, al entrar en contacto con la superficie de separación entre dos medios cambiantes, regresa al punto donde se originó. Ejemplos comunes son la reflexión de la
luz, el
sonido y las ondas en el agua.
La luz es una manifestación de energía. Gracias a ella las imágenes pueden ser reflejadas en un espejo, en la superficie del agua o un suelo muy brillante. Esto se debe a un fenómeno llamado reflexión de la luz. La reflexión ocurre cuando los rayos de luz que inciden en una superficie chocan en ella, se desvían y regresan al medio que salieron formando un ángulo igual al de la luz incidente, muy distinta a la
refracción.
Es el cambio de dirección, en el mismo medio, que experimenta un rayo luminoso al incidir oblicuamente sobre una superficie. Para este caso las leyes de la reflexión son las siguientes:
1a. ley: El rayo incidente, el rayo reflejado y la
normal, se encuentran en un mismo plano.
2a. ley: El ángulo de incidencia es igual al ángulo de reflexión.

θi = θr
Reflexión especular[editar]

Reflejo sobre una burbuja de jabón.
La reflexión especular se produce cuando un rayo de luz incide sobre una superficie pulida (espejo) y cambia su dirección sin cambiar el medio por donde se propaga.
Reflexión difusa[editar]
Cuando un rayo de luz incide sobre una superficie "no pulida", los rayos no se reflejan en ninguna dirección, es decir se difunden. Esto se puede producir por ejemplo en la madera.
Reflexión interna total

Reflexión interna total de la luz.
en fórmula:
 : ángulo crítico;
: ángulo crítico; : índice de refracción.
: índice de refracción.
Retrorreflexión
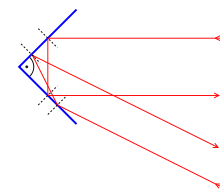
Principio de funcionamiento de un reflector de esquina.
La
retrorreflexión es la capacidad que tienen algunas superficies que por su estructura pueden reflejar la luz de vuelta hacia la fuente, sin que importe el ángulo de incidencia original. Este comportamiento se puede observar en un espejo, pero únicamente cuando éste se encuentra perpendicular a la fuente; es decir, cuando el ángulo de incidencia es igual a 90°. Se puede construir un retrorreflector simple colocando tres espejos ordinarios de forma que todos sean perpendiculares entre sí (un
reflector esquinero). La imagen que se produce es igual a la imagen producida por un espejo pero invertida. Tal como se observa en la figura, la combinación de las diferentes superficies hace que el haz de luz sea reflejado de vuelta a la fuente.
Si a una superficie se le aplica una pequeña capa de esferas reflectivas es posible obtener una superficie con una capacidad limitada de retrorreflexión. El mismo efecto se puede obtener si se dota a la superficies con una estructura similar a pequeñas pirámides (reflexión esquinera). En ambos casos, la estructura interna de la superficie refleja la luz que incide sobre ella y la envía directamente hacia la fuente. Este tipo de superficies se utilizan para crear las señales de tránsito y las placas de los automóviles; en este caso particular no se desea una retrorreflexión perfecta, pues se quiere que la luz retorne tanto hacia las luces del vehículo que emite el haz de luz como a los ojos de la persona que lo va conduciendo.
Reflexión acoplada compleja
La luz se refleja exactamente en la dirección de la fuente de donde proviene debido a un proceso óptico no lineal. En este tipo de reflexión, no solo se invierte la dirección de la luz; también se invierte el frente de la onda. Un reflector acoplado se puede utilizar para eliminar
aberraciones en un haz de luz, reflejándola y haciéndola pasar de nuevo por el dispositivo óptico que causa la aberración.
Reflexión de neutrones
Materiales que reflejan
neutrones, como por ejemplo el
berilio, son utilizados en
reactores nucleares y en
armas atómicas. En las ciencias físicas y químicas, la reflexión de neutrones es utilizada para determinar la estructura y composición interna de un material.
Reflexión del sonido
Cuando una
onda sonora golpea una superficie plana es reflejada de manera coherente asumiendo que el tamaño de la superficie reflectiva es lo suficientemente larga con relación a la longitud de la onda que incide. Tómese en cuenta que las ondas del sonido audible tienen un amplio rango de frecuencias (de 20 Hz hasta 20000 Hz), al igual que la longitud de onda (que pude variar de 20 mm hasta 17 m). Como resultado, se obtiene que la naturaleza en general, así como el comportamiento del fenómeno de reflexión varía de acuerdo con la estructura y la textura de las superficies de reflexión; por ejemplo, una superficie porosa tiende a absorber grandes cantidades de energía, mientras que una superficie áspera (donde áspero es relativo a la longitud de onda) reflejará las ondas en todas direcciones dispersando la energía de la onda, en lugar de reflejar el sonido en forma coherente. Esto nos lleva al campo de la
Acústica arquitectónica, porque la naturaleza de estas reflexiones son críticas para la sensación del espacio en un auditorio.
Reflexión sísmica
Interpretación cuántica
Todas las interacciones entre
fotones y materia se describen como una serie de absorciones y emisiones de
fotones. Cuando un fotón que llega golpea una molécula en la superficie de la materia, es absorbido y casi de inmediato vuelto a emitir. El "nuevo" fotón puede emitirse en cualquier dirección; esto causaría una
reflexión difusa[cita requerida].
La
reflexión especular (siguiendo la ley de la reflexión equi-angular de
Herón) es un efecto de la mecánica cuántica, explicado como la suma de los caminos más probables tomados por los fotones. La interacción con materia liviana es un tópico de la
electrodinámica cuántica, descrita por
Richard Feynman en su libro
QED:La extraña teoría de la luz y la materia. La energía de un fotón que llega a una molécula puede que concuerde con la energía requerida para cambiar el estado de la molécula, causando una transición en el estado cinético,
rotacional,
electrónica o
vibracional de la energía. Cuando esto ocurre, puede que el fotón absorbido no se reemita o puede que se reemita con pérdida de energía. Estos efectos son conocidos como Raman, Brillouin.
Espejo

Vasija reflejada en un espejo.

Reflexión de los rayos de luz en un espejo plano.

Esquema de inversión de la imagen.
Un
espejo (del
lat. specullum)
1 es una superficie pulida en la que, después de incidir, la
luz se refleja siguiendo las leyes de la
reflexión.
El más sencillo es el espejo plano. En este último, un haz de rayos de luz paralelos puede cambiar de dirección completamente en conjunto y continuar siendo un haz de rayos paralelos, pudiendo producir así una
imagen virtual de un objeto con el mismo tamaño y forma que el real. La imagen resulta derecha pero invertida en el eje normal al espejo.
También existen
espejos curvos que pueden ser
cóncavos o
convexos. En un espejo cóncavo cuya superficie forma un
paraboloide de revolución, todos los rayos que inciden paralelos al eje del espejo, se reflejan pasando por el
foco, y los que inciden pasando por el foco, se reflejan paralelos al eje.
Los espejos son objetos que reflejan casi toda la luz que choca contra su superficie debido a este fenómeno podemos observar
nuestra imagen en ellos. Los espejos en realidad son cristales que contienen detrás una capa de aluminio (o de otro material, pero es más fácil de aluminio) y entonces como no puedes ver a través la imagen se ve reflejada como en la primera foto
Historia
Los espejos como utensilios de tocador y objeto manual fueron muy usados en las civilizaciones
egipcia,
griega,
etrusca y
romana. Fue usado en la cultura hebrea, era parte de la fuente de metal que estaba a la entrada del Tabernáculo de la Reunión. Al lavarse los sacerdotes, podían ver sus imperfecciones (Éxodo 38:7-9; 30:18; escrito aproximadamente en el 1447 a. C).
Se elaboraban siempre con metal
bruñido, generalmente
cobre,
plata o
bronce, a este proceso se le conoce como plateo. Tenían forma de placa redonda u oval, decorada ordinariamente con
grabados o
relieves mitológicos en el reverso (los romanos carecen de grabados, pero no de relieves) y con mango tallado para asirlos cómodamente; de ellos, se conservan todavía muchos ejemplares en algunos museos arqueológicos. Durante la alta
Edad Media, apenas se hizo uso del espejo, hasta que en el
siglo XIII se inventó la fabricación de los de
vidrio y de
cristal de roca sobre lámina metálica (o con amalgama de
plomo o
estaño que son los
espejos azogados), sin dejar por esto de construirse los de sólo metal hasta el
siglo XVIII.
El espejo, como mueble de habitación, empieza con el
siglo XVI, pues aunque durante los dos siglos anteriores se citan algunos ejemplares históricos apenas era conocido y su uso era poco corriente. En dicho siglo, se presenta con marco elegante y pie artístico y ocupa lugar distinguido en el
salón como objeto movible y de dimensiones reducidas. Hacia fines del
siglo XVII las fábricas venecianas logran construir espejos de gran tamaño y desde entonces sirven como objetos singularmente decorativos en los salones, en los que ocupan un lugar destacado.
Los espejos modernos consisten en una delgada capa de
plata o
aluminio depositado sobre una plancha de vidrio, la cual protege el metal y hace al espejo más duradero, ver
plateado.
Fórmulas física
«La inversa de la distancia focal es igual a la suma de la inversa de la distancia del objeto al espejo con la inversa de la distancia de la imagen al espejo» y  , en la que m es la magnificación o agrandamiento lateral.
, en la que m es la magnificación o agrandamiento lateral.Para una imagen formada por un espejo parabólico (o esférico de pequeña abertura, donde sea válida la
aproximación paraxial), se cumple que:

, en la que
fes la distancia del foco al espejo,
s la distancia del objeto al espejo, y
s' la distancia de la imagen formada al espejo, se lee:
Folclore
El espejo ocupa un lugar importante en la
mitología y las
supersticiones de muchos pueblos. La imagen que en él se refleja se identifica a menudo con el
alma o
espíritu de la persona: de ahí por ejemplo que los
vampiros, cuerpos sin alma, no se reflejen en él. Cuando un moribundo está a punto de dejar este mundo, es común que se cubran los espejos, por temor a que el alma del agonizante quede encerrada en ellos.
El espejo es también objeto frecuente de consulta: se le juzga capaz de mostrar sucesos y objetos distantes en el tiempo o el espacio. En el cuento de
Blancanieves, el espejo tiene la facultad de hablar y responde a las preguntas que le formula la madrastra.
J. R. R. Tolkien retoma con su célebre «espejo de
Galadriel» la tradición del espejo capaz de mostrar el futuro. En la novela
Harry Potter y la piedra filosofal, de
J. K. Rowling, aparece el
espejo de Oesed (
Deseo leído a la inversa), que no refleja la imagen de quien lo contempla, sino sus deseos más profundos.
También es notable el Espejo de la Sabiduría (en el que se refleja «todas las cosas del cielo y de la tierra excepto el rostro de quien se mira en él»), descrito por
Oscar Wildeen el cuento «
El pescador y su alma».
Refracción
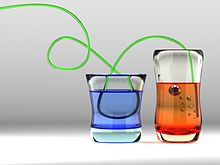
Refracción de la
luz en diversos contenedores.
La
refracción es el cambio de dirección que experimenta una
onda al pasar de un medio material a otro. Solo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si estos tienen
índices de refracción distintos. La refracción se origina en el cambio de
velocidad de propagación de la onda señalada.
Un ejemplo de este fenómeno se ve cuando se sumerge un lápiz en un vaso con agua: el lápiz parece quebrado. También se produce refracción cuando la
luz atraviesa capas de aire a distinta
temperatura, de la que depende el índice de refracción. Los
espejismos son producidos por un caso extremo de refracción, denominado
reflexión total. Aunque el fenómeno de la refracción se observa frecuentemente en ondas electromagnéticas como la luz, el concepto es aplicable a cualquier tipo de onda.
Explicación física
Se produce cuando la
luz pasa de un medio de propagación a otro con una
densidad óptica diferente, sufriendo un cambio de rapidez y un cambio de dirección si no incide perpendicularmente en la superficie. Esta desviación en la dirección de propagación se explica por medio de la
ley de Snell. Esta ley, así como la refracción en medios no homogéneos, son consecuencia del
principio de Fermat, que indica que la luz se propaga entre dos puntos siguiendo la trayectoria de recorrido óptico de menor tiempo.

Lápiz "quebrado" debido a la refracción.
Por otro lado, la velocidad de la penetración de la luz en un medio distinto del vacío está en relación con la longitud de la onda y, cuando un haz de luz blanca pasa de un medio a otro, cada color sufre una ligera desviación. Este fenómeno es conocido como
dispersión de la luz. Por ejemplo, al llegar a un medio más denso, las ondas más cortas pierden velocidad sobre las largas (p. ej., cuando la luz blanca atraviesa un prisma). Las longitudes de onda corta son hasta cuatro veces más dispersadas que las largas lo cual explica que el cielo se vea azulado, ya que para esa gama de colores el índice de refracción es mayor y se dispersa más.
En la refracción se cumplen las leyes deducidas por Huygens que rigen todo el movimiento ondulatorio:
- El rayo incidente, el reflejado y el refractado se encuentran en el mismo plano.
- Los ángulos de incidencia y reflexión son iguales, entendiendo por tales los que forman respectivamente el rayo incidente y el reflejado con la perpendicular (llamada Normal) a la superficie de separación trazada en el punto de incidencia.
La
velocidad de la luz depende del medio por el que viaje, por lo que es más lenta cuanto más denso sea el material y viceversa. Por ello, cuando la luz pasa de un medio menos denso (aire) a otro más denso (cristal), el rayo de luz es refractado acercándose a la normal y por tanto, el ángulo de refracción será más pequeño que el ángulo de incidencia. Del mismo modo, si el rayo de luz pasa de un medio más denso a uno menos denso, será refractado alejándose de la normal y, por tanto, el ángulo de incidencia será menor que el de refracción. Así podemos decir que la refracción es el cambio de dirección de la propagación que experimenta la luz al pasar de un medio a otro.
Índice de refracción
Es la relación entre la velocidad de propagación de la onda en un medio de referencia (por ejemplo el
vacío para las
ondas electromagnéticas) y su velocidad en el medio del que se trate.

Ángulo crítico: cualquier rayo que incida con un ángulo θ
1 mayor al ángulo crítico θ
ccorrespondiente a ese par de sustancias, se
reflejará en la
interfaz en lugar de refractarse.
Refracción de ondas de radio
El fenómeno de la refracción se observa en todo tipo de ondas. En el caso de las ondas de radio, la refracción es especialmente importante en la
ionosfera, en la que se producen una serie continua de refracciones que permiten a las ondas de radio viajar de un punto del planeta a otro.
Refracción de ondas sísmicas
Otro ejemplo de refracción no ligado a
ondas electromagnéticas es el de las
ondas sísmicas. La velocidad de propagación de las ondas sísmicas depende de la
densidad del medio de propagación y, por lo tanto, de la profundidad y de la composición de la región atravesada por las ondas. Se producen fenómenos de refracción en los siguientes casos:
- Refracción entre la transición entre dos capas geológicas, especialmente entre el manto terrestre y el núcleo de la Tierra.
- En el manto, por pequeñas desviaciones de la densidad entre capas ascendentes menos densas y descendentes, más densas.
Ley de refracción (Ley de Snell)
La relación entre el seno del ángulo de incidencia y el seno del
ángulo de refracción es igual a la razón entre la velocidad de la onda en el primer medio y la velocidad de la onda en el segundo medio, o bien puede entenderse como
el producto del índice de refracción del primer medio por el seno del ángulo de incidencia es igual al producto del índice de refracción del segundo medio por el seno del ángulo de refracción, esto es:
 : índice de refracción del primer medio
: índice de refracción del primer medio : ángulo de incidencia
: ángulo de incidencia : índice de refracción del segundo medio
: índice de refracción del segundo medio : ángulo de refracción
: ángulo de refracción
Lente

Tipos principales de lentes.

Las lentes pueden ser usadas para enfocar la luz.
Estrictamente, una
lente óptica es cualquier entidad capaz de desviar los rayos de luz. Las
lentes son objetos transparentes (normalmente de
vidrio), limitados por dos superficies, de las que al menos una es curva. Sin embargo, otros dispositivos como las
lentes de Fresnel, que desvían la luz por medio del fenómeno de difracción, son de gran utilidad y uso por su bajo costo constructivo y el reducido espacio que ocupan.
Las lentes más comunes están basadas en el distinto grado de refracción que experimentan los rayos de luz al incidir en puntos diferentes de su superficie, incluidas las utilizadas para corregir los problemas de visión en
gafas,
anteojos o
lentillas. También se usan lentes, o combinaciones de lentes y
espejos, en
telescopios y
microscopios, con la función de servir como
objetivos o como
oculares. El primer telescopio astronómico fue construido por
Galileo Galilei usando una
lente convergente(lente positiva) como objetivo y otra divergente (lente negativa) como ocular. Existen también instrumentos capaces de hacer converger o divergir otros tipos de
ondas electromagnéticas y a los que se les denomina también lentes. Por ejemplo, en los
microscopios electrónicos las lentes son de carácter magnético.
En
astrofísica es posible observar fenómenos de
lentes gravitatorias, cuando la luz procedente de objetos muy lejanos pasa cerca de objetos masivos, y se curva en su trayectoria.
Etimología
La palabra lente proviene del latín "lens, lentis" que significa "lenteja", por lo que a las lentes ópticas se las denomina así por su parecido con la forma de la legumbre.
En el siglo XIII empezaron a fabricarse pequeños discos de vidrio que podían montarse sobre un marco. Fueron las primeras gafas de libros o gafas de lectura.
La palabra
lente suele ser de género ambiguo. Normalmente se usa en femenino para referirse al cristal óptico, en tanto que en masculino y plural suele reservarse para referirse a las
gafas en algunos países.
Tipos
Las lentes, según la forma que adopten pueden ser convergentes o divergentes.
Las lentes
convergentes (o positivas) son más gruesas por su parte central y más estrechas en los bordes. Se denominan así debido a que unen (convergen), en un punto determinado que se denomina
foco de imagen, todo haz de rayos paralelos al eje principal que pase por ellas. Pueden ser:
- Biconvexas
- Planoconvexas
- Cóncavo-convexas
Las lentes divergentes (o negativas) son más gruesas por los bordes y presentan una estrechez muy pronunciada en el centro. Se denominan así porque hacen divergir (separan) todo haz de rayos paralelos al eje principal que pase por ellas, sus prolongaciones convergen en el foco imagen que está a la izquierda, al contrario que las convergentes, cuyo foco imagen se encuentra a la derecha. Pueden ser:
- Bicóncavas
- Planocóncavas
- Convexo-cóncavas
Lentes artificiales
Se suele denominar lentes artificiales a las construidas con materiales artificiales no homogéneos, de modo que su comportamiento exhibe índices de refracción menores que la unidad (conviene recordar que la
velocidad de fase sí puede ser mayor que la velocidad de la luz en el vacío), con lo que, por ejemplo, se tienen lentes biconvexas divergentes. Nuevamente este tipo de lentes es útil en microondas y sólo últimamente se han descrito materiales con esta propiedad a frecuencias ópticas.
Corriente eléctrica

La corriente eléctrica está definida por convenio en sentido contrario al desplazamiento de los
electrones.

Diagrama del
efecto Hall, mostrando el flujo de
electrones. (en vez de la corriente convencional).
Leyenda:
1. Electrones
2.
Sensor o sonda Hall
3.
Imanes
4.
Campo magnético
5. Fuente de energía
Descripción
En la imagen A, una carga negativa aparece en el borde superior del sensor Hall (simbolizada con el color azul), y una positiva en el borde inferior (color rojo). En B y C, el campo eléctrico o el magnético están invertidos, causando que la polaridad se invierta. Invertir tanto la corriente como el campo magnético (imagen D) causa que la sonda asuma de nuevo una carga negativa en la esquina superior.
El instrumento usado para medir la intensidad de la corriente eléctrica es el
galvanómetro que, calibrado en amperios, se llama
amperímetro, colocado en serie con el conductor por el que circula la corriente que se desea medir.
Historia
Históricamente, la corriente eléctrica se definió como un flujo de cargas positivas y se fijó el sentido convencional de circulación de la corriente, como un flujo de cargas desde el polo positivo al negativo. Sin embargo posteriormente se observó, gracias al
efecto Hall, que en los metales los portadores de carga son negativos,
electrones, los cuales fluyen en sentido contrario al convencional. En conclusión, el sentido convencional y el real son ciertos en tanto que los electrones como protones fluyen desde el polo negativo hasta llegar al positivo (sentido real), cosa que no contradice que dicho movimiento se inicia al lado del polo positivo donde el primer electrón se ve atraído por dicho polo creando un hueco para ser cubierto por otro electrón del siguiente átomo y así sucesivamente hasta llegar al polo negativo (sentido convencional). Es decir la corriente eléctrica es el paso de electrones desde el polo negativo al positivo comenzando dicha progresión en el polo positivo.
2
En el siglo XVIII cuando se hicieron los primeros experimentos con electricidad, sólo se disponía de carga eléctrica generada por frotamiento (
electricidad estática) o por inducción. Se logró (por primera vez, en 1800) tener un movimiento constante de carga cuando el físico italiano
Alessandro Volta inventó la primera pila eléctrica.
Conducción eléctrica
Un material
conductor posee gran cantidad de electrones libres, por lo que es posible el paso de la electricidad a través del mismo. Los electrones libres, aunque existen en el material, no se puede decir que pertenezcan a algún átomo determinado.
Una corriente de electricidad existe en un lugar cuando una carga neta se transporta desde ese lugar a otro en dicha región. Supongamos que la carga se mueve a través de un alambre. Si la carga q se transporta a través de una sección transversal dada del alambre, en un tiempo t, entonces la intensidad de corriente I, a través del alambre es:


Una característica de los electrones libres es que, incluso sin aplicarles un campo eléctrico desde afuera, se mueven a través del objeto de forma aleatoria debido a la energía calórica. En el caso de que no hayan aplicado ningún campo eléctrico, cumplen con la regla de que la media de estos movimientos aleatorios dentro del objeto es igual a cero. Esto es: dado un plano irreal trazado a través del objeto, si sumamos las cargas (electrones) que atraviesan dicho plano en un sentido, y sustraemos las cargas que lo recorren en sentido inverso, estas cantidades se anulan.
Cuando se aplica una fuente de tensión externa (como, por ejemplo, una
batería) a los extremos de un material conductor, se está aplicando un campo eléctrico sobre los electrones libres. Este campo provoca el movimiento de los mismos en dirección al terminal positivo del material (los electrones son atraídos [tomados] por el terminal positivo y rechazados [inyectados] por el negativo). Es decir, los electrones libres son los portadores de la corriente eléctrica en los materiales conductores.
Si la intensidad es constante en el tiempo, se dice que la corriente es
continua; en caso contrario, se llama variable. Si no se produce almacenamiento ni disminución de carga en ningún punto del conductor, la corriente es estacionaria.
Para obtener una corriente de 1 amperio, es necesario que 1
culombio de carga eléctrica por segundo esté atravesando un plano imaginario trazado en el material conductor.
El valor I de la intensidad instantánea será:
Si la intensidad permanece constante, en cuyo caso se denota Im, utilizando incrementos finitos de tiempo se puede definir como:
Si la intensidad es variable la fórmula anterior da el valor medio de la intensidad en el intervalo de tiempo considerado.
Según la
ley de Ohm, la intensidad de la corriente es igual a la tensión (o voltaje) dividido por la resistencia que oponen los cuerpos:
Haciendo referencia a la potencia, la intensidad equivale a la raíz cuadrada de la potencia dividida por la resistencia. En un circuito que contenga varios generadores y receptores, la intensidad es igual a:
donde

es el sumatorio de las fuerzas electromotrices del circuito,

es la suma de todas la fuerzas contraelectromotrices,

es la resistencia equivalente del circuito,
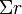
es la suma de las resistencias internas de los generadores y

es el sumatorio de las resistencias internas de los receptores.
Intensidad de corriente en un elemento de volumen:

, donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen de conductor.
[cita requerida]
Definición por medio del magnetismo[editar]

Donde

es la
densidad de corriente de conducción,

es el vector perpendicular al diferencial de superficie,

es el vector unitario normal a la superficie, y

es el diferencial de superficie.
La carga eléctrica puede desplazarse cuando esté en un objeto y éste es movido, como el electróforo. Un objeto se carga o se descarga eléctricamente cuando hay movimiento de carga en su interior.
Corriente continua

Rectificador de corriente alterna en continua, con puente de Gratz. Se emplea cuando la tensión de salida tiene un valor distinto de la tensión de entrada.
Se denomina corriente continua o corriente directa(CC en español, en inglés DC, de Direct Current) al flujo de cargas eléctricas que no cambia de sentido con el tiempo. La corriente eléctrica a través de un material se establece entre dos puntos de distinto potencial. Cuando hay corriente continua, los terminales de mayor y menor potencial no se intercambian entre sí. Es errónea la identificación de la corriente continua con la corriente constante (ninguna lo es, ni siquiera la suministrada por una batería). Es continua toda corriente cuyo sentido de circulación es siempre el mismo, independientemente de su valor absoluto.
Su descubrimiento se remonta a la invención de la primera
pila voltaica por parte del conde y científico italiano
Alessandro Volta. No fue hasta los trabajos de Edison sobre la generación de electricidad, en las postrimerías del siglo XIX, cuando la corriente continua comenzó a emplearse para la transmisión de la energía eléctrica. Ya en el siglo XX este uso decayó en favor de la corriente alterna, que presenta menores pérdidas en la transmisión a largas distancias, si bien se conserva en la conexión de redes eléctricas de diferentes frecuencias y en la transmisión a través de cables submarinos.
Cuando es necesario disponer de corriente continua para el funcionamiento de aparatos electrónicos, se puede transformar la corriente alterna de la red de suministro eléctrico mediante un proceso, denominado rectificación, que se realiza con unos dispositivos llamados
rectificadores, basados en el empleo de
diodos semiconductores o
tiristores (antiguamente, también de
tubos de vacío).
3
Corriente alterna

Voltaje de las fases de un sistema trifásico. Entre cada una de las fases hay un desfase de 120º.

Conexión en
triángulo y en
estrella.
Se denomina corriente alterna (simbolizada CA en español y AC en inglés, de
alternating current) a la corriente eléctrica en la que la magnitud y dirección varían cíclicamente. La forma de onda de la corriente alterna más comúnmente utilizada es la de una onda
sinoidal.
4 En el
uso coloquial, "corriente alterna" se refiere a la forma en la cual la electricidad llega a los hogares y a las empresas.
El sistema usado hoy en día fue ideado fundamentalmente por
Nikola Tesla, y la distribución de la corriente alterna fue comercializada por
George Westinghouse. Otros que contribuyeron al desarrollo y mejora de este sistema fueron
Lucien Gaulard,
John Gibbs y
Oliver Shallenger entre los años 1881 y 1889. La corriente alterna superó las limitaciones que aparecían al emplear la corriente continua (CC), la cual constituye un sistema ineficiente para la distribución de energía a gran escala debido a problemas en la transmisión de potencia.
La razón del amplio uso de la corriente alterna, que minimiza los problemas de trasmisión de potencia, viene determinada por su facilidad de transformación, cualidad de la que carece la corriente continua. La
energía eléctrica trasmitida viene dada por el producto de la
tensión, la intensidad y el tiempo. Dado que la sección de los conductores de las líneas de transporte de energía eléctrica depende de la intensidad, se puede, mediante un
transformador, modificar el voltaje hasta altos valores (
alta tensión), disminuyendo en igual proporción la intensidad de corriente. Esto permite que los conductores sean de menor sección y, por tanto, de menor costo; además, minimiza las pérdidas por
efecto Joule, que dependen del cuadrado de la intensidad. Una vez en el punto de consumo o en sus cercanías, el voltaje puede ser de nuevo reducido para permitir su uso industrial o doméstico de forma cómoda y segura.
Las frecuencias empleadas en las redes de distribución son 50 y 60 Hz. El valor
depende del país.
Corriente trifásica
Se denomina corriente trifásica al conjunto de tres corrientes alternas de igual
frecuencia,
amplitud y
valor eficaz que presentan una diferencia de fase entre ellas de 120°, y están dadas en un orden determinado. Cada una de las corrientes que forman el sistema se designa con el nombre de
fase.
La generación trifásica de energía eléctrica es más común que la monofásica y proporciona un uso más eficiente de los conductores. La utilización de electricidad en forma trifásica es mayoritaria para transportar y distribuir energía eléctrica y para su utilización industrial, incluyendo el accionamiento de motores. Las corrientes trifásicas se generan mediante
alternadores dotados de tres bobinas o grupos de bobinas, arrolladas en un sistema de tres electroimanes equidistantes angularmente entre sí.
Los conductores de los tres electroimanes pueden conectarse en estrella o en triángulo. En la disposición en estrella cada bobina se conecta a una fase en un extremo y a un conductor común en el otro, denominado neutro. Si el sistema está equilibrado, la suma de las corrientes de línea es nula, con lo que el transporte puede ser efectuado usando solamente tres cables. En la disposición en triángulo o delta cada bobina se conecta entre dos hilos de fase, de forma que un extremo de cada bobina está conectado con otro extremo de otra bobina.
El sistema trifásico presenta una serie de ventajas tales como la economía de sus líneas de transporte de energía (hilos más finos que en una línea monofásica equivalente) y de los transformadores utilizados, así como su elevado rendimiento de los receptores, especialmente motores, a los que la línea trifásica alimenta con potencia constante y no pulsada, como en el caso de la línea monofásica.
Tesla fue el inventor que descubrió el principio del campo magnético rotatorio en 1882, el cual es la base de la maquinaria de corriente alterna. Él inventó el sistema de motores y generadores de corriente alterna polifásica que da energía al planeta.
5
Corriente monofásica
Se denomina corriente monofásica a la que se obtiene de tomar una fase de la corriente trifásica y un cable neutro. En España y demás países que utilizan valores similares para la generación y trasmisión de energía eléctrica, este tipo de corriente facilita una tensión de 230 voltios, lo que la hace apropiada para que puedan funcionar adecuadamente la mayoría de electrodomésticos y luminarias que hay en las viviendas.
Desde el centro de transformación más cercano hasta las viviendas se disponen cuatro hilos: un neutro (N) y tres fases (R, S y T). Si la tensión entre dos fases cualesquiera (tensión de línea) es de 400 voltios, entre una fase y el neutro es de 230 voltios. En cada vivienda entra el neutro y una de las fases, conectándose varias viviendas a cada una de las fases y al neutro; esto se llama corriente monofásica. Si en una vivienda hay instalados aparatos de potencia eléctrica alta (aire acondicionado, motores, etc., o si es un taller o una empresa industrial) habitualmente se les suministra directamente corriente trifásica que ofrece una tensión de 400 voltios.
Corriente directa (CD)
Hay dos tipos de corrientes eléctricas que pueden atravesar alambres: corriente directa (CD) y corriente alterna (CA).
La corriente directa (CD) siempre fluye en la misma dirección en un
circuito eléctrico. Los electrones fluyen continuamente en el circuito del terminal negativo de la batería al terminal positivo. Incluso cuando ninguna corriente está atravesando el conductor, los
electrones en el alambre se están moviendo a velocidades de hasta 600 millas (1 000 kilómetros) por segundo, pero en direcciones al azar porque el alambre tiene una temperatura finita. Puesto que un electrón se está moviendo hacia atrás en el conductor al mismo tiempo que otro se está moviendo hacia adelante, ninguna carga neta se transporta a lo largo del circuito. Si se conecta una batería a los extremos del alambre, los electrones son forzados a lo largo del conductor en la misma dirección . La velocidad de los electrones a lo largo del conductor es menor a una pulgada (pocos milímetros) por segundo. De manera que un electrón en específico tarda un largo tiempo en ir alrededor del circuito. Hay tantos electrones que todos están continuamente chocando entre sí, como fichas de dominó, y hay un cambio neto de cargas eléctricas alrededor del circuito que pueden llegar a alcanzar la velocidad de la luz.
Los tomacorrientes en nuestros hogares proporcionan corriente alterna (CA). Los electrones en el alambre cambian de dirección 60 veces por segundo. A los dispositivos eléctricos que usamos no les importa en qué dirección se están moviendo los electrones, puesto que la misma cantidad de corriente atraviesa un circuito sin importar la dirección de la corriente.


- 1. C E T I S 1 0 9{ INTEGRANTES: Lorenzo Pacheco Marco Antonio Martínez Bautista Hermilo Mendoza Torres Christian Antonio Monasterio Vázquez Roberto Joaquín Quintanilla Terán Juan de Dios Silva Flores Miguel Ángel
- 2. Existen muchos circuitos eléctricos que no tienen componentes ni en serie, ni en paralelo, ni mixto. El físico alemán Gustavo Roberto Kirchhoff (1824-1887) propuso unas reglas para el estudio de estas leyes. Aquí sólo se consideran redes con resistencias óhmicas y fuerzas electromotrices (voltajes o tensiones).
- 3. Rama: Es la parte de la red donde circula una corriente de la mismaintensidad.Fijados dos nodos, es un camino a lo largo del circuito que una dichosnodos y que no pase dos veces por el mismo sitio. Hay que darle unsentido
- 4. Nodo: Es un punto de la red donde concurren tres o más conductores oramas.La unión de dos o más terminales- Nodo principal: La unión de tres o más terminales.. es común que se use la sigla LCK para referirse a esta ley. La ley decorrientes de Kirchhoff nos dice que:
- 5. En cualquier nodo, y la suma de todos los nodos y la suma de lascorrientes que entran en ese nodo es igual a la suma de lascorrientes que salen. De igual forma, La suma algebraica de todaslas corrientes que pasan por el nodo es igual a cero
- 6. Si se consideran como positivas las corrientes que llegan a un nodoy como negativas las corrientes que salen, la ley de los nodostambién puede expresarse en la forma siguiente:En un nodo la suma algebraica de las intensidades de la corrientees igual a cero. ∑I = 0 en un nodo cualquiera.
- 7. La primera regla de Kirchhoffequivale a afirmar que la cargaeléctrica ni se crea ni sedestruye (principio deconservación de la cargaeléctrica). Esto significa que lacarga eléctrica no se puedeacumular en un nodo de la red,esto es la cantidad de cargaque entra a un nodo cualquieraen un cierto instante, es igual ala cantidad de carga que salede ese nodo.
- 8. El sentido de la corriente en cada uno delos conductores o ramas se fijaarbitrariamente teniendo en cuenta la leyde los nodos.
- 9. Ley de las mallas:Al recorrer una mallala suma algebraica de las fuerzas electromotrices (e ) y las diferencias de potencial (I .R) en las resistencias es cero. ∑V = 0 en cualquier malla de la red.
- 10. Esta ley es llamada también Segunda leyde Kirchhoff, ley de lazos de Kirchhoff oley de mallas de Kirchhoff y es común quese use la sigla LVK para referirse a esta ley.
- 11. Para aplicar correctamente la ley de Tensiones de Kirchhoff , serecomienda asumir primero un sentido de recorrer la malla. Unavez hecho esto se asigna signos positivos a todas las tensiones deaquellas ramas donde se entre por el terminal positivo en elrecorrido de la malla y se asignasignos negativos cuando entrepor el terminal negativo de la rama.
- 12. Este circuito tiene dos mallasindependientes, por las quesuponemosque circulan lascorrientesI1eI2en el sentido de las agujas delreloj, tal como se indica en la figura.Por el elementoR2circularán tantoI 1 como I 2en sentidos contrarios, por tanto lacorriente real que circula por él es lasuperposición de ambas: I 1-I 2.
- 13. La primera ecuación la obtendremos aplicando la ley deKirchhoff de las tensiones a la primera malla:
- 14. MALLAS Y NODOS MALLAS RAMA NODOS parte de la redla suma algebraica donde circula de las fuerzas y la suma de las corrientes que una corriente deelectromotrices (e ) la mismay las diferencias de entran en ese nodo es igual a intensidad. potencial (I .R) en las resistencias es la suma de las cero. corrientes que salen. LEYES DE KIRCHOFF


Corriente alterna
Se denomina
corriente alterna (abreviada
CA en español y
AC en inglés, de
alternating current) a la
corriente eléctrica en la que la magnitud y el sentido varían cíclicamente.
La forma de oscilación de la corriente alterna más comúnmente utilizada es la oscilación
senoidal con la que se consigue una transmisión más eficiente de la energía, a tal punto que al hablar de corriente alterna se sobrentiende que se refiere a la
corriente alterna senoidal.
Sin embargo, en ciertas aplicaciones se utilizan otras formas de oscilación
periódicas, tales como la triangular o la cuadrada.
Utilizada genéricamente, la CA se refiere a la forma en la cual la electricidad llega a los hogares y a las industrias. Sin embargo, las
señales de audio y de
radiotransmitidas por los
cables eléctricos, son también ejemplos de corriente alterna. En estos usos, el fin más importante suele ser la transmisión y recuperación de la información codificada (o
modulada) sobre la señal de la CA.
Historia
En el año 1882 el físico, matemático, inventor e ingeniero
Nikola Tesla, diseñó y construyó el primer motor de inducción de CA. Posteriormente el físico
William Stanley, reutilizó, en 1885, el principio de inducción para transferir la CA entre dos circuitos eléctricamente aislados. La idea central fue la de enrollar un par de
bobinas en una base de hierro común, denominada bobina de inducción. De este modo se obtuvo lo que sería el precursor del actual
transformador. El sistema usado hoy en día fue ideado fundamentalmente por Nikola Tesla; la distribución de la corriente alterna fue comercializada por
George Westinghouse. Otros que contribuyeron en el desarrollo y mejora de este sistema fueron
Lucien Gaulard,
John Gibbs y
Oliver Shallenger entre los años 1881 y 1889. La corriente alterna superó las limitaciones que aparecían al emplear la corriente continua (CC), que es un sistema ineficiente para la distribución de energía a gran escala debido a problemas en la transmisión de potencia, comercializado en su día con gran agresividad por
Thomas Edison.
La primera transmisión interurbana de la corriente alterna ocurrió en 1891, cerca de
Telluride,
Colorado, a la que siguió algunos meses más tarde otra de Lauffen a Frankfurt en
Alemania. A pesar de las notorias ventajas de la CA frente a la CC, Thomas Edison siguió abogando fuertemente por el uso de la corriente continua, de la que poseía numerosas patentes (véase la
guerra de las corrientes). De hecho, atacó duramente a Nikola Tesla y a George Westinghouse, promotores de la corriente alterna, y a pesar de ello ésta acabó por imponerse. Así, utilizando corriente alterna,
Charles Proteus Steinmetz, de
General Electric, pudo solucionar muchos de los problemas asociados a la producción y transmisión eléctrica, lo que provocó al final la derrota de Edison en la batalla de las corrientes, siendo su vencedor Nikola Tesla y su financiador George Westinghouse.
Corriente alterna frente a corriente continua
La razón del amplio uso de la corriente alterna viene determinada por su facilidad de transformación, cualidad de la que carece la
corriente continua. En el caso de la corriente continua, la elevación de la tensión se logra conectando dínamos en serie, lo que no es muy práctico; al contrario, en corriente alterna se cuenta con un dispositivo: el transformador, que permite elevar la tensión de una forma eficiente.
La
energía eléctrica viene dada por el producto de la
tensión, la
intensidad y el tiempo. Dado que la sección de los conductores de las líneas de transporte de energía eléctrica depende de la intensidad, mediante un
transformador se puede elevar la tensión hasta altos valores (
alta tensión), disminuyendo en igual proporción la intensidad de corriente. Con esto la misma energía puede ser distribuida a largas distancias con bajas intensidades de corriente y, por tanto, con bajas pérdidas por causa del
efecto Joule y otros efectos asociados al paso de corriente, tales como la
histéresis o las
corrientes de Foucault. Una vez en el punto de consumo o en sus cercanías, el voltaje puede ser de nuevo reducido para su uso industrial o doméstico y comercial de forma cómoda y segura.
Las matemáticas y la CA sinusoidal
Algunos tipos de oscilaciones periódicas tienen el inconveniente de no tener definida su expresión matemática, por lo que no se puede operar analíticamente con ellas. Por el contrario, la oscilación sinusoidal no tiene esta indeterminación matemática y presenta las siguientes ventajas:
- La función seno está perfectamente definida mediante su expresión analítica y gráfica. Mediante la teoría de los números complejos se analizan con suma facilidad los circuitos de alterna.
- Las oscilaciones periódicas no sinusoidales se pueden descomponer en suma de una serie de oscilaciones sinusoidales de diferentes frecuencias que reciben el nombre de armónicos. Esto es una aplicación directa de las series de Fourier.
- Se pueden generar con facilidad y en magnitudes de valores elevados para facilitar el transporte de la energía eléctrica.
- Su transformación en otras oscilaciones de distinta magnitud se consigue con facilidad mediante la utilización de transformadores.
Oscilación senoidal
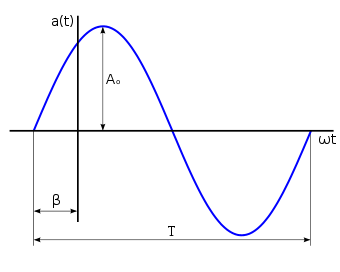
Figura 2: Parámetros característicos de una oscilación sinusoidal.
Una señal senoidal o sinusoidal,

,
tensión,

, o
corriente,

, se puede expresar matemáticamente según sus parámetros característicos (figura 2), como una función del tiempo por medio de la siguiente ecuación:
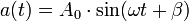
donde
 es la amplitud en voltios o amperios (también llamado valor máximo o de pico),
es la amplitud en voltios o amperios (también llamado valor máximo o de pico), la pulsación en radianes/segundo,
la pulsación en radianes/segundo, el tiempo en segundos, y
el tiempo en segundos, y el ángulo de fase inicial en radianes.
el ángulo de fase inicial en radianes.
Dado que la velocidad angular es más interesante para matemáticos que para ingenieros, la fórmula anterior se suele expresar como:
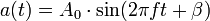
donde
f es la
frecuencia en
hercios (Hz) y equivale a la inversa del período
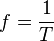
. Los valores más empleados en la distribución son 50 Hz y 60 Hz.
Valores significativos
A continuación se indican otros valores significativos de una señal sinusoidal:
- Valor instantáneo (a(t)): Es el que toma la ordenada en un instante, t, determinado.
- Valor pico a pico (App): Diferencia entre su pico o máximo positivo y su pico negativo. Dado que el valor máximo de sen(x) es +1 y el valor mínimo es -1, una señal sinusoidal que oscila entre +A0 y -A0. El valor de pico a pico, escrito como AP-P, es por lo tanto (+A0)-(-A0) = 2×A0.
- Valor medio (Amed): Valor del área que forma con el eje de abscisas partido por su período. El valor medio se puede interpretar como el componente de continua de la oscilación sinusoidal. El área se considera positiva si está por encima del eje de abscisas y negativa si está por debajo. Como en una señal sinusoidal el semiciclo positivo es idéntico al negativo, su valor medio es nulo. Por eso el valor medio de una Oscilación sinusoidal se refiere a un semiciclo. Mediante el cálculo integral se puede demostrar que su expresión es la siguiente;
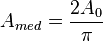
- Pico o cresta: Valor máximo, de signo positivo (+), que toma la oscilación sinusoidal del espectro electromagnético, cada medio ciclo, a partir del punto “0”. Ese valor aumenta o disminuye a medida que la amplitud “A” de la propia oscilación crece o decrece positivamente por encima del valor "0".
- Valor eficaz (A): El valor eficaz se define como el valor de una corriente (o tensión) continua que produce los mismos efectos calóricos que su equivalente de alterna. Es decir que para determinada corriente alterna, su valor eficaz (Ief) será la corriente continua que produzca la misma disipación de potencia (P) en una resistencia(R). Matemáticamente, el valor eficaz de una magnitud variable con el tiempo, se define como la raíz cuadrada de la media de los cuadrados de los valores instantáneos alcanzados durante un período:
-
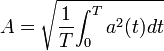
En la literatura inglesa este valor se conoce como R.M.S. (root mean square, valor cuadrático medio), y de hecho en matemáticas a veces es llamado valor cuadrático medio de una función. En el campo industrial, el valor eficaz es de gran importancia, ya que casi todas las operaciones con magnitudes energéticas se hacen con dicho valor. De ahí que por rapidez y claridad se represente con la letra mayúscula de la magnitud que se trate (I, V, P, etc.). Matemáticamente se demuestra que para una corriente alterna sinusoidal el valor eficaz viene dado por la expresión:
-
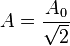
El valor
A, tensión o intensidad, es útil para calcular la potencia consumida por una carga. Así, si una tensión de alterna, desarrolla una cierta potencia P en una carga resistiva dada, una tensión de continua de V
rms desarrollará la misma
potencia P en la misma carga, por lo tanto V
rms x I = V
CA x I (véase
Potencia en corriente alterna)
Representación fasorial
Una función sinusoidal puede ser representada por un
número complejo cuyo argumento crece linealmente con el tiempo(figura 3), al que se denomina
fasor o representación de Fresnel, que tendrá las siguientes características:
- Girará con una velocidad angular ω.
- Su módulo será el valor máximo o el eficaz, según convenga.
La razón de utilizar la representación fasorial está en la simplificación que ello supone. Matemáticamente, un fasor puede ser definido fácilmente por un
número complejo, por lo que puede emplearse la teoría de cálculo de estos números para el análisis de sistemas de corriente alterna.
Consideremos, a modo de ejemplo, una tensión de CA cuyo valor instantáneo sea el siguiente:
Tomando como módulo del fasor su valor eficaz, la representación gráfica de la anterior tensión será la que se puede observar en la figura 4, y se anotará: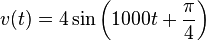
denominadas formas polares, o bien:
denominada forma binómica.
Corriente trifásica
La generación trifásica de energía eléctrica es la forma más común y la que provee un uso más eficiente de los conductores. La utilización de electricidad en forma trifásica es común mayoritariamente para uso en industrias donde muchas de las máquinas funcionan con motores para esta tensión.
La corriente trifásica está formada por un conjunto de tres formas de
oscilación, desfasadas una respecto a la otra 120º (
grados), según el diagrama que se muestra en la figura 5.
Las corrientes trifásicas se generan mediante
alternadores dotados de tres bobinas o grupos de bobinas, enrolladas sobre tres sistemas de piezas polares equidistantes entre sí. El retorno de cada uno de estos
circuitos o fases se acopla en un punto, denominado neutro, donde la suma de las tres corrientes, si el sistema está equilibrado, es cero, con lo que el transporte puede ser efectuado usando solamente tres cables.
Esta disposición sería la denominada conexión en estrella, existiendo también la conexión en triángulo o delta en las que las bobinas se acoplan según esta figura geométrica y los hilos de línea parten de los vértices.
Existen por tanto cuatro posibles interconexiones entre generador y carga:
- Estrella - Estrella
- Estrella - Delta
- Delta - Estrella
- Delta - Delta
En los circuitos tipo
estrella, las corrientes de fase y las corrientes de línea son iguales y, cuando el sistema está equilibrado, las tensiones de línea son
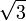
veces mayor que las tensiones de fase y están adelantadas
30° a estas:
-
![V_{linea}=\left[\sqrt {3}V_{fase}\right]_{ \left( \phi + 30 \right)}](https://upload.wikimedia.org/math/2/5/7/257c1358a03ca56ff2a02477bb70e35d.png)
En los circuitos tipo
triángulo o
delta, pasa lo contrario, las tensiones de fase y de línea, son iguales y, cuando el sistema está equilibrado, la corriente de fase es
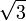
veces más pequeña que la corriente de línea y está adelantada
30° a ésta:
Circuito RL
Un
circuito RL es un
circuito eléctrico que contiene una
resistencia y una
bobina en serie. Se dice que la bobina se opone transitoriamente al establecimiento de una corriente en el circuito.
La ecuación diferencial que rige el circuito es la siguiente:

Donde:
Régimen transitorio[editar]


Dónde:
La constante de tiempo

caracteriza la « duración » del régimen transitorio. Así, la corriente permanente del circuito se establece a 99% después de una duración de 5

.
Cuando la corriente se convierte en permanente, la ecuación se simplifica en

, ya que

.
Régimen sinusoidal permanente[editar]
Circuito RC

Circuito RC en configuración paso bajo.
En la configuración de paso bajo la señal de salida del circuito se coge en bornes del condensador, estando este conectado en serie con la resistencia. En cambio en la configuración de paso alto la tensión de salida es la caída de tensión en la resistencia.
Este mismo circuito tiene además una utilidad de regulación de tensión, y en tal caso se encuentran configuraciones en paralelo de ambos, la resistencia y el condensador, o alternativamente, como limitador de subidas y bajas bruscas de tensión con una configuración de ambos componentes en serie. Un ejemplo de esto es el circuito Snubber.
Comportamiento en el dominio del tiempo
Carga
El sistema reaccionará de distinta manera de acuerdo a las excitaciones entrantes, como ejemplo, podemos representar la respuesta a la función escalón o la función de salto. La tensión originalmente desde el tiempo 0 subirá hasta que tenga la misma que la fuente, es decir,

. La corriente entrará en el condensador hasta que entre las placas ya no puedan almacenar más carga por estar en equilibrio electrostático (es decir que tengan la misma tensión que la fuente). De esta forma una placa quedará con carga positiva y la otra con carga negativa, pues esta última tendrá un exceso de electrones.
El tiempo de carga del circuito es proporcional a la magnitud de la resistencia eléctrica
R y la capacidad
C del condensador. El producto de la resistencia por la capacidad se llama
constante de tiempo del circuito y tiene un papel muy importante en el comportamiento de este.
 .
.

Teóricamente este proceso es infinitamente largo, hasta que U(t)=Umax. En la práctica se considera que el tiempo de carga tL se mide cuando el condensador se encuentra aproximadamente en la tensión a cargar (más del 99% de ésta), es decir, aproximadamente 5 veces su constante de tiempo.

La constante de tiempo τ marca el tiempo en el que la curva tangente en el inicio de la carga marca en intersección con la línea de máxima tensión la constante de tiempo τ. Este tiempo sería el tiempo en el que el condensador alcanzaría su tensión máxima si es que la corriente entrante fuera constante. En la realidad, la corriente con una fuente de tensión constante tendrá un carácter exponencial, igual que la tensión en el condensador.
La máxima corriente

fluye cuando el tiempo es inicial(es decir t=0). Esto es debido que el condensador está descargado, y la corriente que fluye se calcula fácilmente a través de la ley de Ohm, con:

Respuesta natural[editar]
El circuito RC más simple que existe consiste en un condensador y una resistencia en
serie. Cuando un circuito consiste solo de un
condensador cargado y una
resistencia, el condensador descargará su energía almacenada a través de la resistencia. La tensión o diferencia de potencial eléctrico a través del condensador, que depende del tiempo, puede hallarse utilizando la
ley de Kirchhoff de la corriente, donde la corriente a través del condensador debe ser igual a la corriente a través de la resistencia. Esto resulta en la
ecuación diferencial lineal:
 .
.
Resolviendo esta ecuación para
V se obtiene la fórmula de decaimiento
exponencial:

donde
V0 es la tensión o diferencia de potencial eléctrico entre las placas del
condensador en el tiempo
t = 0.
El tiempo requerido para que el voltaje caiga hasta

es denominado "constante de tiempo RC" y es dado por

Impedancia compleja[editar]


donde
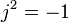
Circuito en serie[editar]

 .
.
Funciones de transferencia[editar]
 .
.
De forma similar, la función de transferencia desde el voltaje de entrada al voltaje de la resistencia es
 .
.
Polos y ceros[editar]
Ambas funciones de transferencia tienen un único
polo localizado en
 .
.
Ganancia y fase[editar]
La magnitud de las ganancias a través de los dos componentes son:

y
 ,
,
y los ángulos de fase son:

y
 .
.
Estas expresiones conjuntamente pueden ser sustituidas en la usual expresión para la representación por
fasores:

 .
.
La corriente en el circuito es la misma en todos los puntos del circuito ya que el circuito está en serie:

Respuesta a impulso[editar]
La respuesta impulso para el voltaje del condensador es


De forma similar, la respuesta impulso para el voltaje de la
resistencia es

Análisis de frecuencia[editar]

Lugar de Bode de

Un análisis de frecuencia del montaje permite determinar cuáles son las
frecuencias que el fitro rechaza y cuáles acepta. Para bajas frecuencias,

tiene un módulo cercano a 1 y una fase próxima a 0. Cuando la frecuencia aumenta, su módulo disminuye para tender a 0 mientras que la fase tiende a

. Por el contrario,

posee un módulo cercano a 0 a bajas frecuencias y una fase próxima a
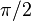
y cuando la frecuencia aumenta, el módulo tiende a 1 y su fase tiende a 0.
Cuando

:
 y
y  .
. y
y  .
.
Cuando

:
 y
y 
 y
y  .
.
Así, cuando la salida del filtro está tomada sobre el condensador el comportamiento es de tipo
filtro paso bajo: las altas frecuencias son atenuadas y las bajas frecuencias pasan. Si la salida está tomada sobre la resistencia, se produce el proceso inverso y el circuito se como un
filtro paso alto.
La
frecuencia de corte 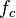
del circuito que define el límite tiene 3 dB entre las frecuencias atenuadas y aquéllas que no lo son; es igual a:
 (en Hz)
(en Hz)
Análisis temporal[editar]
Por razones de simplicidad, el análisis temporal se efectuará utilizando la
transformada de Laplace p. Suponiendo que el circuito está sometido a una
escalón de tensión de amplitud
V de entrada (

para

y

sinon) :


 .
.
La transformada de Laplace inversa de estas expresiones resulta:

 .
.
En este caso, el condensador se carga y la tensión en los bornes tiende a V, mientras que en los bornes de la
resistencia tiende a 0.

Determinación gráfica de

para la observación de

.
El circuito RC posee una
constante de tiempo, generalmente expresado como

, que representa el tiempo que toma la tensión para efectuar el 63% (

) de la variación necesaria para pasar del valor inicial al final.

 .
.
Las soluciones son exactamente las mismas que aquéllas obtenidas mediante la transformada de Laplace.
A alta frecuencia, es decir cuando

, el condensador no tiene tiempo suficiente para cargarse y la tensión en los bornes permanece pequeña.
Así:

y la intensidad en el circuito vale por tanto:
 .
.
Como,

se obtiene:
 .
.
La tensión en los bornes del condensador integrado se comporta como un filtro de paso-bajo.
A baja frecuencia, es decir cuando

, el condensador tiene el tiempo de cargarse casi completamente.
Entonces,


Ahora,

 .
.
La tensión en los bornes de la resistencia derivado se comporta como un filtro de paso-alto.
Circuito en paralelo[editar]

Un circuito RC en paralelo.
El circuito RC en
paralelo generalmente es de menor interés que el circuito en serie. Esto es en gran parte debido a que la tensión de salida

es igual a la tensión de entrada

— como resultado, el circuito no actúa como filtro de la señal de entrada si no es alimentado por una
fuente de corriente.
Con impedancias complejas:

y
 .
.
Esto muestra que la corriente en el
condensador está desfasada 90º de fase con la
resistencia (y la fuente de corriente). Alternativamente, las ecuaciones diferenciales de gobierno que pueden usarse son:

y
 .
.
Cuando es alimentado por una fuente de corriente, la función de transferencia de un circuito RC en paralelo es:
 .
.
Resonancia en un circuito RLC serie
Cuando se conecta un circuito RLC en serie, alimentado por una señal alterna (fuente de tensión de
corriente alterna), hay un efecto de ésta en cada uno de los componentes.
En el condensador aparecerá una reactancia capacitiva, y en la bobina una reactancia inductiva, dadas por las siguientes fórmulas: XL = 2 x π x f x L y XC = 1 / (2 x π x f x C), donde:
- π = 3.14159
- f = frecuencia en Hertz
- L = Valor de la bobina en henrios
- C = Valor del condensador en faradios
Como se puede ver los valores de estas reactancias depende de la frecuencia de la fuente. A mayor frecuencia, XL es mayor, pero XC es menor y viceversa. Hay una frecuencia para la cual el valor de la XC y XL son iguales. Esta frecuencia se llama frecuencia de resonancia y se obtiene de la siguiente fórmula: FR = 1 / (2 x π x (L x C)1/2)
En
resonancia como los valores de XC y XL son iguales, se cancelan y en un
circuito RLC en serie la
impedancia que ve la fuente es el valor de la
resistencia. A frecuencias menores a la de resonancia, el valor de la reactancia capacitiva es grande y la impedancia es capacitiva. A frecuencias superiores a la de resonancia, el valor de la reactancia inductiva crece y la impedancia es inductiva.
Nota: es importante visualizar que los efectos de la reactancia capacitiva y la inductiva son opuestos, es por eso que se cancelan y causan la oscilación (resonancia).
El Ancho de banda (BW) y el Factor de calidad (Q)
Los circuitos resonantes son utilizados para seleccionar bandas de frecuencias y para rechazar otras. Cuando se está en la frecuencia de resonancia la
corriente por el circuito es máxima.
En la figura: A una corriente menor (70.7% de la máxima), la frecuencia F1 se llama frecuencia baja de corte o frecuencia baja de potencia media. La frecuencia alta de corte o alta de potencia media es F2.
El ancho de banda de este circuito está entre estas dos frecuencias y se obtiene con la siguiente fórmula:
- Ancho Banda = BW = F2 – F1
- El factor de calidad (Q) o factor Q es: Q = XL/R o XC/R
También la relacionándolo con el Ancho Banda: Resonancia en un circuito RLC serie. Q = frecuencia resonancia / Ancho banda = FR/BW
Ejemplos:
- Si F1 = 50 Khz y F2 = 80 Khz, FR = 65 Khz, el factor de calidad es: Q = FR / BW = 65 / (80-50) = 2.17
- Si F1 = 60 Khz y F2 = 70 Khz, FR = 65 Khz, el factor de calidad es: Q = FR / BW = 65 / (70-60) = 6.5
Se puede observar que el factor de calidad es mejor a menor ancho de banda. (el circuito es más selectivo)
Tut_resonanciaSerie.asp
 Para fines del siglo XIX, se sabía que la radiación de cuerpo negro se debía a las oscilaciones de las partículas cargadas de la superficie de estos cuerpos. Sin embargo, a partir del electromagnetismo clásico era imposible deducir los espectros y las leyes experimentales de Stefan-Boltzmann y de Wien. La Física clásica había llegado a un límite que no podría superar.
Para fines del siglo XIX, se sabía que la radiación de cuerpo negro se debía a las oscilaciones de las partículas cargadas de la superficie de estos cuerpos. Sin embargo, a partir del electromagnetismo clásico era imposible deducir los espectros y las leyes experimentales de Stefan-Boltzmann y de Wien. La Física clásica había llegado a un límite que no podría superar.
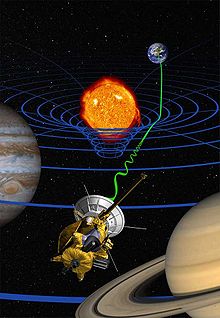














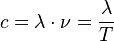



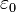 ) y magnéticas (
) y magnéticas ( ) por parte de la teoría de
) por parte de la teoría de 

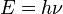
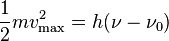

 ) entre un
) entre un 











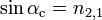
 : ángulo crítico;
: ángulo crítico; : índice de refracción.
: índice de refracción.







 , en la que fes la distancia del foco al espejo, s la distancia del objeto al espejo, y s' la distancia de la imagen formada al espejo, se lee:
, en la que fes la distancia del foco al espejo, s la distancia del objeto al espejo, y s' la distancia de la imagen formada al espejo, se lee:





 : índice de refracción del primer medio
: índice de refracción del primer medio : ángulo de incidencia
: ángulo de incidencia : índice de refracción del segundo medio
: índice de refracción del segundo medio : ángulo de refracción
: ángulo de refracción








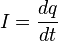
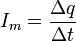
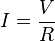
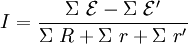
 es el sumatorio de las fuerzas electromotrices del circuito,
es el sumatorio de las fuerzas electromotrices del circuito,  es la suma de todas la fuerzas contraelectromotrices,
es la suma de todas la fuerzas contraelectromotrices,  es la resistencia equivalente del circuito,
es la resistencia equivalente del circuito,  es la suma de las resistencias internas de los generadores y
es la suma de las resistencias internas de los generadores y  es el sumatorio de las resistencias internas de los receptores.
es el sumatorio de las resistencias internas de los receptores. , donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen de conductor.[
, donde encontramos n como el número de cargas portadoras por unidad de volumen dV; q refiriéndose a la carga del portador; v la velocidad del portador y finalmente dS como el área de la sección del elemento de volumen de conductor.[
 es la
es la  es el vector perpendicular al diferencial de superficie,
es el vector perpendicular al diferencial de superficie,  es el vector unitario normal a la superficie, y
es el vector unitario normal a la superficie, y  es el diferencial de superficie.
es el diferencial de superficie.



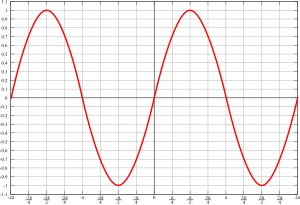

 ,
,  , o
, o  , se puede expresar matemáticamente según sus parámetros característicos (figura 2), como una función del tiempo por medio de la siguiente ecuación:
, se puede expresar matemáticamente según sus parámetros característicos (figura 2), como una función del tiempo por medio de la siguiente ecuación: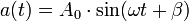
 es la amplitud en
es la amplitud en  la
la  el tiempo en
el tiempo en  el ángulo de fase inicial en radianes.
el ángulo de fase inicial en radianes.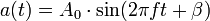
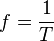 . Los valores más empleados en la distribución son 50 Hz y 60 Hz.
. Los valores más empleados en la distribución son 50 Hz y 60 Hz.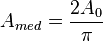
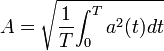
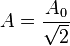
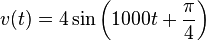
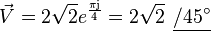
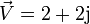
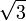 veces mayor que las tensiones de fase y están adelantadas 30° a estas:
veces mayor que las tensiones de fase y están adelantadas 30° a estas:![V_{linea}=\left[\sqrt {3}V_{fase}\right]_{ \left( \phi + 30 \right)}](https://upload.wikimedia.org/math/2/5/7/257c1358a03ca56ff2a02477bb70e35d.png)


 es la
es la  es la
es la  es la
es la 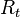 es la
es la  , es:
, es:

 es la intensidad de la
es la intensidad de la  es la
es la  , ya que
, ya que  .
. de valor
de valor  .
.
 . La corriente entrará en el condensador hasta que entre las placas ya no puedan almacenar más carga por estar en equilibrio electrostático (es decir que tengan la misma tensión que la fuente). De esta forma una placa quedará con carga positiva y la otra con carga negativa, pues esta última tendrá un exceso de electrones.
. La corriente entrará en el condensador hasta que entre las placas ya no puedan almacenar más carga por estar en equilibrio electrostático (es decir que tengan la misma tensión que la fuente). De esta forma una placa quedará con carga positiva y la otra con carga negativa, pues esta última tendrá un exceso de electrones.

 fluye cuando el tiempo es inicial(es decir t=0). Esto es debido que el condensador está descargado, y la corriente que fluye se calcula fácilmente a través de la ley de Ohm, con:
fluye cuando el tiempo es inicial(es decir t=0). Esto es debido que el condensador está descargado, y la corriente que fluye se calcula fácilmente a través de la ley de Ohm, con:
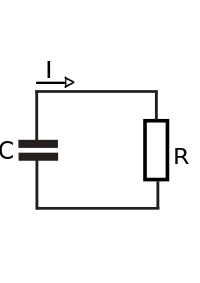
 .
.
 es denominado "constante de tiempo RC" y es dado por
es denominado "constante de tiempo RC" y es dado por


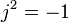
 es el decrecimiento
es el decrecimiento 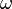 es la
es la 

 .
. .
. .
. .
.
 ,
,
 .
.
 .
.





 . Por el contrario,
. Por el contrario,  posee un módulo cercano a 0 a bajas frecuencias y una fase próxima a
posee un módulo cercano a 0 a bajas frecuencias y una fase próxima a 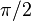 y cuando la frecuencia aumenta, el módulo tiende a 1 y su fase tiende a 0.
y cuando la frecuencia aumenta, el módulo tiende a 1 y su fase tiende a 0. :
: y
y  .
. y
y  .
. :
: y
y 
 y
y  .
.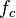 del circuito que define el límite tiene 3 dB entre las frecuencias atenuadas y aquéllas que no lo son; es igual a:
del circuito que define el límite tiene 3 dB entre las frecuencias atenuadas y aquéllas que no lo son; es igual a: (en
(en  para
para  y
y  sinon) :
sinon) :

 .
.
 .
.
 .
. , que representa el tiempo que toma la tensión para efectuar el 63% (
, que representa el tiempo que toma la tensión para efectuar el 63% ( ) de la variación necesaria para pasar del valor inicial al final.
) de la variación necesaria para pasar del valor inicial al final.
 .
. , el condensador no tiene tiempo suficiente para cargarse y la tensión en los bornes permanece pequeña.
, el condensador no tiene tiempo suficiente para cargarse y la tensión en los bornes permanece pequeña.
 .
.
 .
. , el condensador tiene el tiempo de cargarse casi completamente.
, el condensador tiene el tiempo de cargarse casi completamente.


 .
.
 es igual a la tensión de entrada
es igual a la tensión de entrada  — como resultado, el circuito no actúa como filtro de la señal de entrada si no es alimentado por una
— como resultado, el circuito no actúa como filtro de la señal de entrada si no es alimentado por una 
 .
.
 .
. .
.