Gasto Volumétrico

Que es?
Es la relación existente entre el volumen de
liquido que fluye por un conducto y el tiempo que tarda en fluir.
G= V/t
G= Gasto en m3/s
V= Volumen del liquido que fluye en metros cúbicos
(m3)
t= Tiempo que tarda en fluir el liquido en segundos
(s)
Formulas
u
El Gasto también puede calcularse si se conoce la velocidad del liquido
y el área de la sección transversal de la tubería.
u
V= Avt
u
G= Avt/t
u
G= Av
u
Donde:
G= Gasto en m3/s
v= velocidad del liquido en m/s
A= área de la sección transversal del tubo en
metros cuadrados (m2)
1) Calcular el gasto de agua por una tubería al
circular 1.5 m3 en ¼ de minuto
Datos Formula Sustitucion y Resultado
G=? G=
V/t G= 1.5 m3/15seg
V=1.5
m3
G= 0.1 m3/Seg
t= 15 seg.
Problemas
u
2) Calcular el tiempo que tardara en llenarse un tanque cuya capacidad
es 10m3 al suministrar un gasto de 40l/seg
u
Datos Formula Conversión de unidades
u t=? T=V/G 40l/seg x 1 m3/1000l
= 0.04 m3/seg
u
V= 10 m3
u
G= 40l/Seg
Solución y Resultado t=
10m3/0.04 m3/s
t=250 Seg.
Teorema de Bernoulli
El principio de Bernoulli, también
denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el
comportamiento de un fluido en reposo moviéndose a lo largo de
una corriente de agua.
u
Un liquido ideal cuyo flujo es estacionario, la suma de la energía
cinetica, potencial y de presión que tiene el liquido en un punto es igual a la
suma de estas energías en otro punto cualquiera.
u
El liquido tiene, tanto en el punto 1 como en el punto 2, tres tipos de
energía:
u
A) Energia Cinetica: debido a la velocidad y la masa del liquido Ec= mv2/2
u
B) Energia Potencial: Debido a la altura del liquido, respecto a un
punto de referencia Ep= mgh
u
C) Energía de Presión: Originada por la presión que las moléculas del
liquido ejercen entre si, por lo cual el trabajo realizado para el
desplazamiento de las moléculas es igual a la energía de presión.
u
Epresion = Pm/p
u
Donde:
u
Epresion: Energía de presión en JOULES
u
P: Presion en N/m2
u
m: masa del liquido en kilogramos
u
p: Densidad del liquido en KG/m3
u
De acuerdo con el teorema de BERNOULLI, la suma de las energías
cinética, potencia y de Presión en le punto 1 es igual a la suma de estas
energías en el punto 2.
u Ec1 + Ep1
+Epresion1 = Ec2 + Ep2 + Epresion2
u mv2 + mgh
+ Pm/p = mv2 + mgh + Pm/p
Si dividimos la expresión anterior entre la masa se
obtine la ecuacion correspondiente para expresar la energía por unidad de masa:
V2/2 + gh
+ P/p = V2/2 + gh + P/p
Ecuación de continuidad
Cuando un fluido fluye por un conducto de diámetro
variable, su velocidad cambia debido a que la sección transversal varía de una
sección del conducto a otra.
En todo fluido incompresible, con flujo
estacionario (en régimen laminar), la velocidad de un punto cualquiera de un
conducto es inversamente proporcional a la superficie, en ese punto, de la
sección transversal de la misma.
Que es la ecuación de continuidad y donde:
S es la superficie de las secciones transversales
de los puntos 1 y 2 del conducto.
v es la velocidad del flujo en los puntos 1 y 2 de
la tubería.
La ecuación de continuidad no es más que un caso
particular del principio de conservación de la masa. Se basa en que el caudal
(Q) del fluido ha de permanecer constante a lo largo de toda la conducción.
Dado que el caudal es el producto de la superficie
de una sección del conducto por la velocidad con que fluye el fluido, tendremos
que en dos puntos de una misma tubería se debe cumplir que:
Es decir la velocidad en el estrechamiento aumenta de forma
proporcional a lo que se reduce la sección.
En la imagen de la derecha puedes ver como la sección se reduce de A1
a A2. Teniendo en cuenta la ecuación anterior:
Se puede concluir que puesto que el caudal debe mantenerse constante a
lo largo de todo el conducto, cuando la sección disminuye, la velocidad del
flujo aumenta en la misma proporción y viceversa.
|
TEOREMA DE TORRICELLI
TEOREMA DE TORRICELLI
El teorema de Torricelli o principio de
Torricelli es una aplicación del principio de Bernoulli y estudia el flujo
de un líquido contenido en un
recipiente, a través de un pequeño orificio, bajo la acción de
la gravedad.
Problemas:
Un disque
tiene una fuga en un punto de 20 metros bajo la superficie
Cual es la
velocidad de salida?
Determinar el
caudal de un fluido hidraulico que sircula por una tuberia con un
Diametro
interior de 30mm sabiendo que su velocidad
es de 4m/s. expresalo en m3
Y en min.
TEMPERATURA
La
temperatura es una propiedad física e intensiva de la materia. La temperatura
no depende de la cantidad de materia ni promueve el cambio estructural de la
misma. La temperatura mide en cierta manera la energía asociada al movimiento o
energía cinética de las partículas que componen la materia bajo estudio.
En
la actualidad se utilizan comúnmente tres unidades de medida: los grados
Fahrenheit (°F), del sistema inglés, los Kelvin (K), del sistema Internacional
y los grados Celsius (°C), unidad derivada de los Kelvin.
La
escala Kelvin es similar a la escala Celsius. En ambas se divide en cien
pedazos iguales el intervalo entre la temperatura a la que se congela ya a la
que se evapora el agua. La única diferencia real entre las dos escalas
son los valores en los cuales ocurren estos eventos. Por ejemplo, en la
escala Celsius se asigna el valor de 0 al punto de congelación del agua,
mientras que en la escala Kelvin se asigna el valor de 273.15K. Por otro lado
en la escala Celsius se asigna el valor de 100°C al punto de evaporación de
agua, mientras que en la escala Kelvin se asigna el 373.15K.

Para convertir de un sistema a otro hay que recordar
que:
Temperatura en Kelvin = Temperatura en °C + 273.15
Temperatura en °C = Temperatura en Kelvin – 273.15
Temperatura en °C = Temperatura en Kelvin – 273.15
En ecuaciones sería así:

En contraste a las escalas
Celsius y Kelvin, en la escala Fahrenheit el intervalo entre la temperatura de
congelación y la de evaporación del agua se divide en 180 intervalos iguales.
Al punto de congelación del agua se le asigna 32°F y al punto de ebullición
212°F. Utilizando la ecuación de la pendiente podemos obtener que cada grado
Celsius equivale a 1.8 grados Fahrenheit.

Así que:
Temperatura en °F = (9/5 x
Temperatura en °C) + 32
Temperatura en °C = 5/9 x (Temperatura en °F – 32)
Temperatura en °C = 5/9 x (Temperatura en °F – 32)
En ecuaciones se
escribirían:

Ejemplo:
El punto de fusión de la sal
de mesa ocurre a los 1,474°F. Expresa esta temperatura en Celsius y en
Kelvin.
Solución:
Solución:
Primero convertiremos de
Fahrenheit a Celsius
°C = 5/9 x (°F – 32)
°C = 5/9 x (1474 – 32)
°C = 5/9 x 1442
°C = 801°C
°C = 5/9 x (°F – 32)
°C = 5/9 x (1474 – 32)
°C = 5/9 x 1442
°C = 801°C
Ahora convertiremos de
Celsius a Kelvin
K = °C + 273.15
K = 801 + 273.15
K = 1,074 K
K = °C + 273.15
K = 801 + 273.15
K = 1,074 K
ESCALAS
TERMOMETRICAS
LAS
PRINCIPALES ESCALAS TEMPERATURAS SON:
Ø
Escala Fahrenheit.
Ø
Escala CELCIUS.
Ø
Escala absoluta o KELVIN.
Ñ
INSTRUMENTOS DE MEDICIÓN
Ñ
TERMOMETROS DE VIDRIO
Ñ
TERMOMETROS DE RESISTENCIA (CONOCIDOS COMO TERMISTORES)
Ñ
TERMOPARES
Ñ
PIROMETROS
ESCALA
FAHRENHEIT
La escala Fahrenheit toma como cero una
temperatura que está por debajo del punto de fusión del hielo, por lo tanto
para el hielo indica una temperatura de 32º F.
Para el agua hirviendo o vapor indica 212º F.
 Para
pasar de Fahrenheit a grados Celsius usamos la siguiente fórmula:
Para
pasar de Fahrenheit a grados Celsius usamos la siguiente fórmula:
u
 Para
pasar a grados Kelvin usamos la siguiente:
Para
pasar a grados Kelvin usamos la siguiente:
 Para
pasar a grados Kelvin usamos la siguiente:
Para
pasar a grados Kelvin usamos la siguiente:
u
ESCALA CELCIUS
La escala Celsius toma como cero la
temperatura del punto de fusión del hielo, por lo tanto para el hielo indica
una temperatura de 0 ºC.
Para el agua hirviendo o vapor indica 100 ºC.
Para pasar de grados Celsius a Fahrenheit
usamos la siguiente fórmula:
Para pasar a grados Kelvin usamos esta:
ESCALA KELVIN
La escala Kelvin toma como cero la temperatura del gas ideal a volumen
cero, por lo tanto para el hielo indica una temperatura de 273 ºK.
Para el agua hirviendo o vapor indica 373 ºK.
Para pasar de grados Kelvin a Fahrenheit usamos la siguiente fórmula:
Para pasar a grados Celsius usamos esta:
 |
||
 |
||
Dilatómetro antiguo.
Se
denomina dilatación térmica al aumento de longitud, volumen o alguna otra dimensión
métrica que sufre un cuerpo físico debido al aumento de temperatura que se
provoca en él por cualquier medio. La contracción térmica es
la disminución de propiedades métricas por disminución de la misma.
Índice
Es aquella
en la cual predomina la variación en una única dimensión, o sea, en el ancho,
largo o altura del cuerpo. El coeficiente de dilatación lineal, designado por αL,
para una dimensión lineal cualquiera, se puede medir experimentalmente
comparando el valor de dicha magnitud antes y después:
Donde , es el
incremento de su integridad física cuando se aplica un pequeño cambio global y
uniforme de temperatura a todo
el cuerpo. El cambio total de longitud de la dimensión lineal que se considere,
puede despejarse de la ecuación anterior:
Donde:
α=coeficiente
de dilatación lineal [°C-1]
L0 =
Longitud inicial
Lf =
Longitud final
T0 =
Temperatura inicial.
Tf =
Temperatura final

Dilatación térmica
Se denomina dilatación térmica al aumento de longitud, volumen o alguna otra dimensión métrica que sufre un cuerpo físico debido al aumento de temperatura que se provoca en él por cualquier medio. La contracción térmica es la disminución de propiedades métricas por disminución de la misma.
Dilatación lineal[editar]
Es aquella en la cual predomina la variación en una única dimensión, o sea, en el ancho, largo o altura del cuerpo. El coeficiente de dilatación lineal, designado por αL, para una dimensión lineal cualquiera, se puede medir experimentalmente comparando el valor de dicha magnitud antes y después:
Donde  , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 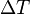 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
 , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 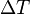 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
Donde:
- α=coeficiente de dilatación lineal [°C-1]
- L0 = Longitud inicial
- Lf = Longitud final
- T0 = Temperatura inicial.
- Tf = Temperatura final
Dilatación volumétrica[editar]
Es el coeficiente de dilatación volumétrico, designado por αV, se mide experimentalmente comparando el valor del volumen total de un cuerpo antes y después de cierto cambio de temperatura como, y se encuentra que en primera aproximación viene dado por:
Experimentalmente se encuentra que un sólido isótropo tiene un coeficiente de dilatación volumétrico que es aproximadamente tres veces el coeficiente de dilatación lineal. Esto puede probarse a partir de la teoría de la elasticidad lineal. Por ejemplo si se considera un pequeño prisma rectangular (de dimensiones: Lx, Ly y Lz), y se somete a un incremento uniforme de temperatura, el cambio de volumen vendrá dado por el cambio de dimensiones lineales en cada dirección:
 Esta última relación prueba que
Esta última relación prueba que 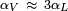 , es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
, es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.Dilatación de área[editar]
Cuando un área o superficie se dilata, lo hace incrementando sus dimensiones en la misma proporción. Por ejemplo, una lámina metálica aumenta su largo y ancho, lo que significa un incremento de área. La dilatación de área se diferencia de la dilatación lineal porque implica un incremento de área.
El coeficiente de dilatación de área es el incremento de área que experimenta un cuerpo de determinada sustancia, de área igual a la unidad, al elevarse su temperatura un grado centígrado. Este coeficiente se representa con la letra griega gamma (γ). El coeficiente de dilatación de área se usa para los sólidos. Si se conoce el coeficiente de dilatación lineal de un sólido, su coeficiente de dilatación de área será dos veces mayor:
Al conocer el coeficiente de dilatación de área de un cuerpo sólido se puede calcular el área final que tendrá al variar su temperatura con la siguiente expresión:
Donde:
- γ=coeficiente de dilatación de área [°C-1]
- A0 = Área inicial
- Af = Área final
- T0 = Temperatura inicial.
- Tf = Temperatura final

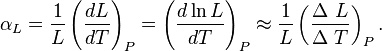
![L_f = L_0 [1 +\alpha_L (T_f - T_0)]\;](https://upload.wikimedia.org/math/4/d/8/4d8d9e521d59aa36de0d776706db3b16.png)

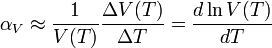

![A_f = A_0 [1 +\gamma_A (T_f - T_0)]\;](https://upload.wikimedia.org/math/8/4/4/84444b9c6e865aaf0b6d1376be7a9a6b.png)
No hay comentarios:
Publicar un comentario